Question

【题目】解下列方程或方程组：

① 2( x 2) 3(4 x 1) 9(1 x)

②

③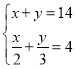

④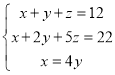

Answer 1

【答案】①；②；③；④

【解析】

①先去括号、移项得到2x-12x+9x=9+4-3，然后合并后把x的系数化为1即可；

②先把方程两边乘以12得3（x-1）-12=2（2x+1），然后去括号、移项、合并，再把x的系数化为1；

③先把方程整理为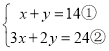，然后利用加减消元法解方程；

④先把第三个方程分别代入第一个和第二个方程得到关于y和z的二元一次方程组，解二元一次方程组得到y和z的值，然后利用代入法求出x的值．

解：①去括号得2x-4-12x+3=9-9x，
移项得2x-12x+9x=9+4-3，
合并得-x=10，
系数化为1得x=-10；

②去分母得3（x-1）-12=2（2x+1），
去括号得3x-3-12=4x+2，
移项得3x-4x=2+3+12，
合并得-x=17，
系数化为1得x=-17；

③原方程组整理为，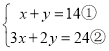

①×3-②得y=18，
把y=0代入①得x=-4，
所以原方程组的解为；

④，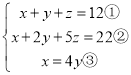

把③代入①得5y+z=12，
把③代入②得6y+5z=22，

解方程组，得，

把y=2代入③得x=8，

所以原方程组的解为.