题目内容
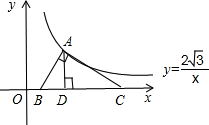 如图,线段AB=2,且与x轴成60°的角,点C在x轴上,AB⊥AC于A,AD⊥BC于D.
如图,线段AB=2,且与x轴成60°的角,点C在x轴上,AB⊥AC于A,AD⊥BC于D.(1)求AD的长;
(2)若点A在反比例函数y=
2
| ||
| x |
分析:(1)要求AD的长,知道∠ABD=60°在Rt△ABD中利用勾股定理可以求得.
(2)要求C的坐标,只要求出OC的长度就可以,可以先求出点A的坐标而求出OD的长,再在直角三角形ADC中求出DC的长就得知C的坐标.
(2)要求C的坐标,只要求出OC的长度就可以,可以先求出点A的坐标而求出OD的长,再在直角三角形ADC中求出DC的长就得知C的坐标.
解答:解:(1)∵△ABD是直角三角形,∠ABD=60°,
∴∠BAD=30°,
∴BD=
AB=1.
由勾股定理得AD=
,
∴点A的纵坐标为
;
(2)设A(a,
)在双曲线上.
∴
=
,
∴a=2,
∴OD=2.
∵AB⊥AC,
∴△ABC是直角三角形,且∠ABD=60°,
∴∠ACB=30°,在直角三角形ADC中由够勾股定理得DC=3,
∴OC=5,
∴C(5,0).
∴∠BAD=30°,
∴BD=
| 1 |
| 2 |
由勾股定理得AD=
| 3 |
∴点A的纵坐标为
| 3 |
(2)设A(a,
| 3 |
∴
| 3 |
2
| ||
| a |
∴a=2,
∴OD=2.
∵AB⊥AC,
∴△ABC是直角三角形,且∠ABD=60°,
∴∠ACB=30°,在直角三角形ADC中由够勾股定理得DC=3,
∴OC=5,
∴C(5,0).
点评:本题是反比例函数的一道综合试题,考查了勾股定理的运用,运用待定系数法求点的坐标等知识点.

练习册系列答案
相关题目
 21、如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30度.BD是⊙O的切线吗?请说明理由.
21、如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30度.BD是⊙O的切线吗?请说明理由. (2013•呼伦贝尔)如图,线段AB、DC分别表示甲乙两座建筑物的高,AB⊥BC,DC⊥BC,两建筑物的水平距离BC为30米,若甲建筑物的高AB=28米,在点A处观察乙建筑物顶部D的仰角为60°,求乙建筑物的高度 (结果保留1位小数,
(2013•呼伦贝尔)如图,线段AB、DC分别表示甲乙两座建筑物的高,AB⊥BC,DC⊥BC,两建筑物的水平距离BC为30米,若甲建筑物的高AB=28米,在点A处观察乙建筑物顶部D的仰角为60°,求乙建筑物的高度 (结果保留1位小数, 如图,线段AB长为2米,AB⊥MN,垂足为A,一动点P从点A出发,以1米/秒的速度向射线AM方向移动.设移动的时间为x(秒).
如图,线段AB长为2米,AB⊥MN,垂足为A,一动点P从点A出发,以1米/秒的速度向射线AM方向移动.设移动的时间为x(秒). 如图,线段AB上有5个点C,D,E,F,G,则图中线段的条数有( )
如图,线段AB上有5个点C,D,E,F,G,则图中线段的条数有( )