��Ŀ����
��ͼ1��������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�A��x���ϣ���C��y����������ϣ��߶�OA��OC��
��OA��OC���Ƿ���x2-5x+4=0�����������������ߵĶԳ�����ֱ��x=
��
��1���������ߵĽ���ʽ��
��2�����߶�BC���Ƿ����һ��D��ʹ��S��ACD��S��ABD=2��1�������ڣ����������D�ķ����������Ľ���ʽ���������ڣ�˵�����ɣ�
��3����ͼ2��һ������P��OC���е�M�������ȵ���x���ϵ�ij�㣨��Ϊ��E�����ٵ��������߶Գ����ϵ�ij�㣨��Ϊ��F��������˶�����C�����P�˶������·������

��OA��OC���Ƿ���x2-5x+4=0�����������������ߵĶԳ�����ֱ��x=
| 5 |
| 2 |
��1���������ߵĽ���ʽ��
��2�����߶�BC���Ƿ����һ��D��ʹ��S��ACD��S��ABD=2��1�������ڣ����������D�ķ����������Ľ���ʽ���������ڣ�˵�����ɣ�
��3����ͼ2��һ������P��OC���е�M�������ȵ���x���ϵ�ij�㣨��Ϊ��E�����ٵ��������߶Գ����ϵ�ij�㣨��Ϊ��F��������˶�����C�����P�˶������·������

���㣺���κ����ۺ���
ר�⣺
��������1�����Ƚⷽ�̵ó�AO��CO�ij��������ó�A��C������꣬�������������ߵĶԳ�����ֱ��x=
���������ʽ���ɣ�
��2������S��ACD��S��ABD=2��1����������ͬ�ߵó�CD��BD=2��1�������������������ε����ʵó�D�����꣬���ɵó���������������ʽ��
��3����������֮���߶���̺���ԳƵ���������⣮����C�����ֱ��x=
�ĶԳƵ�C�䣬��M�����x��ĶԳƵ�M�䣬����C��M�䣮��ôE��F����ֱ��C��M����x��������߶Գ���Ľ��㣬������ȼ��ɣ�
| 5 |
| 2 |
��2������S��ACD��S��ABD=2��1����������ͬ�ߵó�CD��BD=2��1�������������������ε����ʵó�D�����꣬���ɵó���������������ʽ��
��3����������֮���߶���̺���ԳƵ���������⣮����C�����ֱ��x=
| 5 |
| 2 |
��� �⣺��1�����߶�OA��OC�ij��ȣ�OA��OC���Ƿ���x2-5x+4=0����������
�⣺��1�����߶�OA��OC�ij��ȣ�OA��OC���Ƿ���x2-5x+4=0����������
���ã�OA=1��CO=4��
��A����������-1��0������0��4����
�������ߵĶԳ�����ֱ��x=
��
��-
=
��
�ɵã�
��
��ã�
��
�������ߵĽ���ʽΪ��y=-
x2+
x+4��
��2�����ڣ�
���ɣ�����ADAC������D��DE��y���ڵ�E��DF��x���ڵ�F��
��S��ACD��S��ABD=2��1��D���߶�BC�ϣ�
��CD��BD=2��1��
������ɵó���ED��BO��
���CED�ס�COB��
��
=
��
��
=
��
��ã�DE=4��
ͬ���ɵó���
=
=
��
��DF=
��
��D����������4��
��
�辭����D�ķ����������Ľ���ʽΪ��y=
��
��k=4��
=
��
�෴���������Ľ���ʽΪ��y=
��
��3����C�����ֱ��x=
�ĶԳƵ�C�䣬��M�����x��ĶԳƵ�M�䣬����C��M�䣮
��E��F�ֱ�Ϊֱ��C��M����x��������߶Գ���Ľ��㣬��ʱC'M'��Ϊ��P�˶������·������
����C�䣨5��4����M�䣨0��-2����
�ʵ�P�˶������·����=C'M'=
=
��
 �⣺��1�����߶�OA��OC�ij��ȣ�OA��OC���Ƿ���x2-5x+4=0����������
�⣺��1�����߶�OA��OC�ij��ȣ�OA��OC���Ƿ���x2-5x+4=0�������������ã�OA=1��CO=4��
��A����������-1��0������0��4����
�������ߵĶԳ�����ֱ��x=
| 5 |
| 2 |
��-
| b |
| 2a |
| 5 |
| 2 |
�ɵã�
|
��ã�
|
�������ߵĽ���ʽΪ��y=-
| 2 |
| 3 |
| 10 |
| 3 |
��2�����ڣ�
���ɣ�����ADAC������D��DE��y���ڵ�E��DF��x���ڵ�F��
��S��ACD��S��ABD=2��1��D���߶�BC�ϣ�
��CD��BD=2��1��
������ɵó���ED��BO��
���CED�ס�COB��
��
| CD |
| BC |
| ED |
| BO |
��
| 2 |
| 3 |
| ED |
| 6 |
��ã�DE=4��
ͬ���ɵó���
| DF |
| CO |
| BD |
| BC |
| 1 |
| 3 |
��DF=
| 4 |
| 3 |
��D����������4��
| 4 |
| 3 |
�辭����D�ķ����������Ľ���ʽΪ��y=
| k |
| x |
��k=4��
| 4 |
| 3 |
| 16 |
| 3 |
�෴���������Ľ���ʽΪ��y=
| 16 |
| 3x |
��3����C�����ֱ��x=
| 5 |
| 2 |
��E��F�ֱ�Ϊֱ��C��M����x��������߶Գ���Ľ��㣬��ʱC'M'��Ϊ��P�˶������·������
����C�䣨5��4����M�䣨0��-2����
�ʵ�P�˶������·����=C'M'=
| C��C2+M��C2 |
| 61 |
������������Ҫ�����˷�������������ʽ���Լ�����ϵ��������κ�������ʽ�Լ����öԳ�����Сֵ�����Լ����������ε��ж������ʵ�֪ʶ���������Ƶó�D�������ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��֪��ABC����ACB��ƽ����CD��AB�ڵ�D��DE��BC�������E�DZ�AC���е㣬AC=5cm����DE�ij���
��֪��ABC����ACB��ƽ����CD��AB�ڵ�D��DE��BC�������E�DZ�AC���е㣬AC=5cm����DE�ij���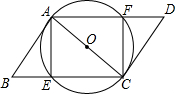 ��ͼ��AC�ǡ�O��ֱ�����ı���ABCD��ƽ���ı��Σ�AD��BC�ֱ�O�ڵ�F��E������AE��CF��
��ͼ��AC�ǡ�O��ֱ�����ı���ABCD��ƽ���ı��Σ�AD��BC�ֱ�O�ڵ�F��E������AE��CF�� ��ͼ����ƽ��ֱ������ϵ�У�������
��ͼ����ƽ��ֱ������ϵ�У�������
 ��ͼ���ڵȱ�������ABC�У���ABC����ACB��ƽ���߽��ڵ�F������F��DE��BC���ֱ���AB��AC���ڵ�D��E��
��ͼ���ڵȱ�������ABC�У���ABC����ACB��ƽ���߽��ڵ�F������F��DE��BC���ֱ���AB��AC���ڵ�D��E��