题目内容
9.如果n是正整数,且a=-1,那么-a2n+1=1.分析 先判断出2n+1的奇偶性,然后进行计算即可.
解答 解:∵n是正整数,
∴2n+1为奇数.
∵-1的奇次幂是-1,
∴-a2n+1=-(-1)=1.
故答案为:1.
点评 本题主要考查的是有理数的乘方,判断出2n+1的奇偶性是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
17. 如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
 如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B等于( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
19.对于抛物线y=-$\frac{1}{2}$(x+1)2+3,下列结论不正确的是( )
| A. | 抛物线的开口向下 | |
| B. | 对称轴为直线x=1 | |
| C. | 顶点坐标为(-1,3) | |
| D. | 此抛物线是由y=-$\frac{1}{2}$x2+3向左平移1个单位得到的 |
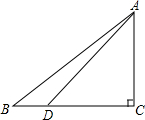 如图,在Rt△ABC中,∠C=90°,sin=$\frac{3}{5}$,点D在BC边上,DC=AC=6.
如图,在Rt△ABC中,∠C=90°,sin=$\frac{3}{5}$,点D在BC边上,DC=AC=6. 已知D、E两点在△ABC内,求作一点P,使PE=PD,且点P到∠B两边的距离相等(尺规作图,保留作图痕迹).
已知D、E两点在△ABC内,求作一点P,使PE=PD,且点P到∠B两边的距离相等(尺规作图,保留作图痕迹).