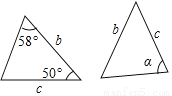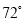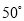题目内容
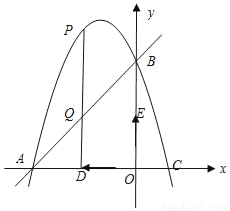
如图,抛物线经过点A(﹣3,0)、B(0,3),C(1,0).
(1)求抛物线及直线AB的函数关系式;
(2)有两动点D、E同时从O出发,以每秒1个单位长度的相同的速度分别沿线段OA、OB向A、B做匀速运动,过D作PD⊥OA分别交抛物线和直线AB于P、Q,设运动时间为t(0<t<3).
①求线段PQ的长度的最大值;
②连接PE,当t为何值时,四边形DOEP是正方形;
③连接DE,在运动过程中,是否存在这样的t值,使PE=DE?若存在,请求出t的值;若不存在,请说明理由.
练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目


 x﹣
x﹣ 分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
 =0.2,
=0.2,  =0.5,则设两人中成绩更稳定的是_____(填“甲”或“乙”)
=0.5,则设两人中成绩更稳定的是_____(填“甲”或“乙”)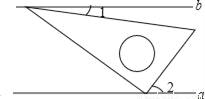

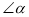 的度数是
的度数是