题目内容
 如图,△ABC的高BD与CE相交于点O,OD=OE,AO的延长线交BC于点M,请你从图中找出几对全等的直角三角形,并说明理由.
如图,△ABC的高BD与CE相交于点O,OD=OE,AO的延长线交BC于点M,请你从图中找出几对全等的直角三角形,并说明理由.考点:直角三角形全等的判定
专题:
分析:△ADO≌△AEO,△DOC≌△EOB,△COF≌△BOF,△ACF≌△ABF,△ADB≌△AEC,△BCE≌△CBD.利用全等三角形的判定可证明,做题时,要结合已知条件与三角形全等的判定方法逐个验证.
解答:解:△ADO≌△AEO,△DOC≌△EOB,△COF≌△BOF,△ACF≌△ABF,△ADB≌△AEC,△BCE≌△CBD.理由如下:
在△ADO与△AEO中,∠ADO=∠AEO=90°,
,
∴△ADO≌△AEO(HL),
∴∠DAO=∠EAO,AD=AE.
在△DOC与△EOB中,
,
∴△DOC≌△EOB(ASA),
∴DC=EB,OC=OB,
∴DC+AD=EB+AE,即AC=AB,
∵∠DAO=∠EAO,
∴AM⊥BC,CM=BM.
在△COF与△BOF中,∠OMC=∠OMB=90°,
,
∴△COF≌△BOF(HL).
在△ACF与△ABF中,∠AFC=∠AFB=90°,
,
∴△ACF≌△ABF(HL).
在△ADB与△AEC中,
,
∴△ADB≌△AEC(SAS).
在△BCE与△CBD中,∠BEC=∠CDB=90°,
,
∴△BCE≌△CBD(HL).
在△ADO与△AEO中,∠ADO=∠AEO=90°,
|
∴△ADO≌△AEO(HL),
∴∠DAO=∠EAO,AD=AE.
在△DOC与△EOB中,
|
∴△DOC≌△EOB(ASA),
∴DC=EB,OC=OB,
∴DC+AD=EB+AE,即AC=AB,
∵∠DAO=∠EAO,
∴AM⊥BC,CM=BM.
在△COF与△BOF中,∠OMC=∠OMB=90°,
|
∴△COF≌△BOF(HL).
在△ACF与△ABF中,∠AFC=∠AFB=90°,
|
∴△ACF≌△ABF(HL).
在△ADB与△AEC中,
|
∴△ADB≌△AEC(SAS).
在△BCE与△CBD中,∠BEC=∠CDB=90°,
|
∴△BCE≌△CBD(HL).
点评:本题主要考查了直角三角形全等的判定方法,判定两个直角三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
下列各式不能分解因式的是( )
| A、3x2-4x |
| B、x2+y2 |
| C、x2+2x+1 |
| D、9-x2 |
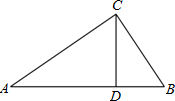 如图,Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=16,BC=12,求CD的长.
如图,Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=16,BC=12,求CD的长.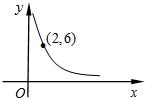 如图是反比例函数y=
如图是反比例函数y=