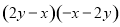题目内容
2.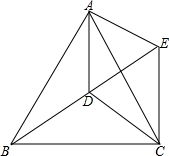 如图所示,点D是等边三角形ABC内一点,DA=13,DB=19,DC=21,将△ABD绕点A逆时针旋转到△ACE的位置,求△DEC的周长.
如图所示,点D是等边三角形ABC内一点,DA=13,DB=19,DC=21,将△ABD绕点A逆时针旋转到△ACE的位置,求△DEC的周长.
分析 由等边三角形的性质得出∠BAC=60°,由旋转的性质得出△ACE≌△ABD,得出AE=AD,CE=DB=19,∠EAC=∠DAB,证出∠DAE=60°,得出△ADE是等边三角形,因此DE=AD=13,即可求出△DEC的周长.
解答 解:∵△ABC是等边三角形,
∴∠BAC=60°,
由旋转的性质得:△ACE≌△ABD,
∴AE=AD=13,CE=DB=19,∠EAC=∠DAB,
∴∠EAC+∠DAC=∠DAB+∠DAC=∠BAC=60°,
即∠DAE=60°,
∴△ADE是等边三角形,
∴DE=AD=13,
∴△DEC的周长=DE+DC+CE=13+21+19=53.
点评 本题考查等边三角形的性质与判定、旋转的性质、全等三角形的性质;熟练掌握等边三角形和旋转的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
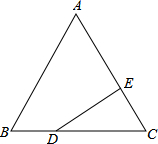 等边△ABC中,BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,求证:DE⊥AC.
等边△ABC中,BD=$\frac{1}{3}$BC,CE=$\frac{1}{3}$AC,求证:DE⊥AC.
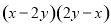 B.
B. 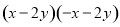
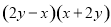 D.
D.