题目内容
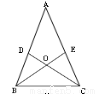
如图，在△ABC中，AB=AC，∠A=36°，两条角平分线BE、CD相交于点O，则图中全等等腰三角形有
A．1对 B．2对 C．3对 D．4对
C
【解析】
试题分析：因为AB=AC，∠A=36°，所以∠ABC=∠ACB=72°,而BE、CD是角平分线，所以∠ABE=∠EBC=∠ACD=∠DCB=36°,所以可得△ABE≌△ACD,所以BD=CE,进而可得△BDO≌△CEO,△BDC≌△CEB,由此共三对全等等腰三角形.
考点：三角形全等的判定.
练习册系列答案
相关题目
≈1.732）
中分母化整数，其结果应为（ ）
－（4k+1)x+3k+3=0．
B.
C.
D.