题目内容
15.化简:($\frac{2}{3}$a2b-$\frac{1}{9}$a2b6)÷(-$\frac{1}{3}$ab)=$-2a+\frac{1}{3}a{b}^{5}$.分析 此题直接利用多项式除以单项式的法则即可求出结果.
解答 解:$(\frac{2}{3}{a^2}b-\frac{1}{9}{a^2}{b^6})÷(-\frac{1}{3}ab)$=$-2a+\frac{1}{3}a{b}^{5}$.
故答案为:$-2a+\frac{1}{3}a{b}^{5}$.
点评 本题考查多项式除以单项式.多项式除以单项式,先把多项式的每一项都分别除以这个单项式,然后再把所得的商相加.

练习册系列答案
相关题目
5.(-0.125)2008×82008+(-1)2008+(-1)2009的值是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
10.下列变形是因式分解的是( )
| A. | x(x+1)=x2+x | B. | x2+2x+1=(x+1)2 | C. | x2+xy-3=x(x+y)-3 | D. | x2+6x+4=(x+3)2-5 |
7.在函数$y=\sqrt{3-x}+\frac{1}{{\sqrt{2x-1}}}$中,自变量x的取值范围是( )
| A. | $\frac{1}{2}<x≤3$ | B. | $\frac{1}{2}≤x≤3$ | C. | x≤3且$x≠\frac{1}{2}$ | D. | $\frac{1}{2}<x<3$ |
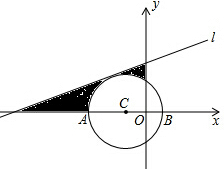 已知:如图,以C(-1,0)为圆心,2为半径的圆与x轴交于A、B,直线l的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$
已知:如图,以C(-1,0)为圆心,2为半径的圆与x轴交于A、B,直线l的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$ 已知,如图,在△ABC中,∠BAC=80°,AD⊥BC于D,AE平分∠DAC,∠B=60°,求∠AED.
已知,如图,在△ABC中,∠BAC=80°,AD⊥BC于D,AE平分∠DAC,∠B=60°,求∠AED.