题目内容
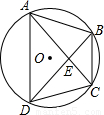
(2000•广西)如图,⊙O1与⊙O2相交于A、B两点,BO2切⊙O1于点B,BO2的延长线交⊙O2于点D,DA的延长线交⊙O1于点C.(1)证明:DB⊥BC;
(2)如果AC=3AD,求∠C的度数;
(3)在(2)的情况下,若⊙O2的半径为6,求四边形O1O2CD的面积.
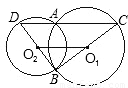
【答案】分析:(1)连接AB,可证得BA⊥CD,由BC是⊙O1的切线,根据切线的性质推出DB⊥BC;
(2)由AC=3AD;得AD= DC,由切割线定理得出BD=
DC,由切割线定理得出BD= DC,则∠C=30°;
DC,则∠C=30°;
(3)先求出⊙O1的半径,AB、CD的长,由三角形的中位线定理求得O1O2的长,再求四边形O1O2CD的面积.
解答: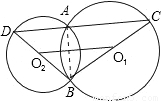 (1)证明:连接AB,∵BC是⊙O1的直径,
(1)证明:连接AB,∵BC是⊙O1的直径,
∴BA⊥CD,(1分)
所以BD是⊙O2的直径.(2分)
又∵BD是⊙O1的切线,所以DB⊥BC.(3分)
(2)解:∵AC=3AD;
∴AD= DC,
DC,
∵BD2=DA•DC= DC2,(5分)
DC2,(5分)
∴BD= DC,(6分)
DC,(6分)
∴∠C=30°.(7分)
(3)解:设⊙O1、⊙O2的半径分别为r1、r2.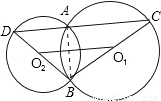
∵⊙O2的半径为6,
∴AB=6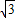 ,
,
∴r1=6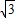 ,(9分)
,(9分)
∴AC=18,
∴AD=6,
∵O1O2是△BCD的中位线,O1O2= DC=12,(11分)
DC=12,(11分)
 AB=3
AB=3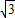 ,
,
∴S梯形O1O2CD= (24+12)×3
(24+12)×3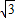 =54
=54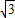 .(12分)
.(12分)
点评:本题考查了切线的性质、切割定理和三角形的中位线定理,难度较大.
(2)由AC=3AD;得AD=
 DC,由切割线定理得出BD=
DC,由切割线定理得出BD= DC,则∠C=30°;
DC,则∠C=30°;(3)先求出⊙O1的半径,AB、CD的长,由三角形的中位线定理求得O1O2的长,再求四边形O1O2CD的面积.
解答:
 (1)证明:连接AB,∵BC是⊙O1的直径,
(1)证明:连接AB,∵BC是⊙O1的直径,∴BA⊥CD,(1分)
所以BD是⊙O2的直径.(2分)
又∵BD是⊙O1的切线,所以DB⊥BC.(3分)
(2)解:∵AC=3AD;
∴AD=
 DC,
DC,∵BD2=DA•DC=
 DC2,(5分)
DC2,(5分)∴BD=
 DC,(6分)
DC,(6分)∴∠C=30°.(7分)
(3)解:设⊙O1、⊙O2的半径分别为r1、r2.

∵⊙O2的半径为6,
∴AB=6
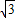 ,
,∴r1=6
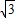 ,(9分)
,(9分)∴AC=18,
∴AD=6,
∵O1O2是△BCD的中位线,O1O2=
 DC=12,(11分)
DC=12,(11分) AB=3
AB=3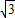 ,
,∴S梯形O1O2CD=
 (24+12)×3
(24+12)×3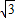 =54
=54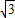 .(12分)
.(12分)点评:本题考查了切线的性质、切割定理和三角形的中位线定理,难度较大.

练习册系列答案
相关题目