题目内容
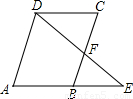
（2000•广西）如图，?ABCD中，E是AB延长线上一点，DE交BC于点F，已知BE：AB=2：3，S△BEF=4，求S△CDF．
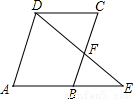
【答案】分析：根据平行四边形的性质，可证△BEF∽△CDF，由BE：AB=2：3，可证BE：DC=2：3，根据相似三角形的性质，可证S△DCF=（
）2•S△BEF=
×4=9．
解答：解：∵四边形ABCD是平行四边形，
∴AE∥DC，
∴△BEF∽△CDF，（3分）
∵AB=DC，BE：AB=2：3，
∴BE：DC=2：3，（5分）
∴S△DCF=（
）2•S△BEF=
×4=9．（7分）
点评：本题主要考查了相似三角形的判定和性质，平行四边形的性质等知识点．
）2•S△BEF=×4=9．解答：解：∵四边形ABCD是平行四边形，
∴AE∥DC，
∴△BEF∽△CDF，（3分）
∵AB=DC，BE：AB=2：3，
∴BE：DC=2：3，（5分）
∴S△DCF=（
）2•S△BEF=×4=9．（7分）点评：本题主要考查了相似三角形的判定和性质，平行四边形的性质等知识点．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
