题目内容
15. 反比例函数y=$\frac{k}{x}$在第一象限内的图象如图,MP垂直x轴于点P,如果△MOP的面积为3,那么k的值是6.
反比例函数y=$\frac{k}{x}$在第一象限内的图象如图,MP垂直x轴于点P,如果△MOP的面积为3,那么k的值是6.
分析 先设反比例函数得解析式为y=$\frac{k}{x}$(k≠0),再根据△AOB的面积为3求出|k|的值,由其函数图象在第一象限可知k>0,进而可确定出k的值.
解答 解:设反比例函数得解析式为y=$\frac{k}{x}$(k≠0),
∵△MPO的面积为3,
∴|k|=6,
∵其函数图象在第一象限,
∴k>0,
∴k=6.
故答案为:6.
点评 本题考查的是反比例函数系数k的几何意义,即反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是 $\frac{|k|}{2}$,且保持不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.某电动车销售点销售低档、高档两种型号的电动车,每台进价分别为1800元、2700元,下表是近两个月的销售情况:
(注:进价、售价均保持不变,利润=销售收入-进货成本)
(1)求低、高档两种型号的电动车的销售单价;
(2)若该销售点准备用不多于11.7万元的金额再采购这两种型号的电动车共50台,求高档电动车最多能采购多少台;
(3)在(2)的条件下,该销售点销售完这50台电动车能否实现利润为1.4万元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
| 月份 | 销售数量(台) | 销售收入(万元) | |
| 低档 | 高档 | ||
| 3月 | 10 | 10 | 5 |
| 4月 | 15 | 20 | 9 |
(1)求低、高档两种型号的电动车的销售单价;
(2)若该销售点准备用不多于11.7万元的金额再采购这两种型号的电动车共50台,求高档电动车最多能采购多少台;
(3)在(2)的条件下,该销售点销售完这50台电动车能否实现利润为1.4万元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
10.在平行四边形ABCD中,如果∠A=50°,那么∠D=( )
| A. | 40° | B. | 50° | C. | 130° | D. | 不能确定 |
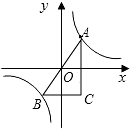 如图,点A(2,y)是反比例函数y=$\frac{12}{x}$的图象上一点,延长AO交该图象于点B,AC⊥x轴,BC⊥y轴,求△ABC的面积.
如图,点A(2,y)是反比例函数y=$\frac{12}{x}$的图象上一点,延长AO交该图象于点B,AC⊥x轴,BC⊥y轴,求△ABC的面积. 如图,矩形ABCD中,AB=6,BC=10.请你设计一种方案,把此矩形剪成两块,并拼成一个菱形(要求在原图上画出分割线,并画出拼后的菱形,标上字母和能反映剪拼方法的数据).
如图,矩形ABCD中,AB=6,BC=10.请你设计一种方案,把此矩形剪成两块,并拼成一个菱形(要求在原图上画出分割线,并画出拼后的菱形,标上字母和能反映剪拼方法的数据).