题目内容
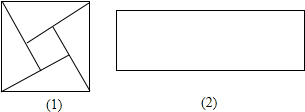
现有四块直角边为a，b，斜边为c的直角三角形的纸板，我们可以从中取出若干块拼图（需画出所拼的图形）然后证明勾股定理．如拼成下图，可利用相等面积关系证明勾股定理．
（1）利用所拼的图形证明勾股定理；
（2）请你再拼一个图形，然后通过上述的方法证明勾股定理．
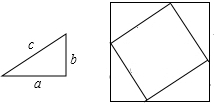
解：（1）解法一：①如图：
②证明：∵大正方形的面积表示为（a+b）2，大正方形的面积也可表示为c2+4×
ab，
∴（a+b）2=c2+4×ab，
a2+b2+2ab=c2+2ab
∴a2+b2=c2，
即直角三角形两直角边的平方和等于斜边的平方．
解法二：①如图
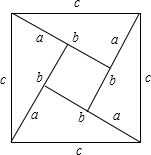
②证明：∵大正方形的面积表示为：c2，
又可以表示为：ab×4+（b-a）2，
∴c2=b×4+（b-a）2，c2=2ab+b2-2ab+a2，
∴c2=a2+b2，
即直角三角形两直角边的平方和等于斜边的平方．
分析：勾股定理的证明可以通过图形的面积之间的关系来完成．
点评：此题考查的知识点勾股定理的证明，关键利用三角形和正方形边长的关系进行组合图形，利用面积的关系证明勾股定理．
②证明：∵大正方形的面积表示为（a+b）2，大正方形的面积也可表示为c2+4×
ab，∴（a+b）2=c2+4×
ab，a2+b2+2ab=c2+2ab
∴a2+b2=c2，
即直角三角形两直角边的平方和等于斜边的平方．
解法二：①如图
②证明：∵大正方形的面积表示为：c2，
又可以表示为：
ab×4+（b-a）2，∴c2=
b×4+（b-a）2，c2=2ab+b2-2ab+a2，∴c2=a2+b2，
即直角三角形两直角边的平方和等于斜边的平方．
分析：勾股定理的证明可以通过图形的面积之间的关系来完成．
点评：此题考查的知识点勾股定理的证明，关键利用三角形和正方形边长的关系进行组合图形，利用面积的关系证明勾股定理．
练习册系列答案
相关题目
