题目内容
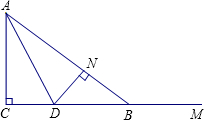
如图,已知AC⊥CM,点B是射线CM上一点(点B不与点C重合),AC=4,∠CAB的平分线 AD与射线CM交于点D,过点D作DN⊥AB,垂足为N.
AD与射线CM交于点D,过点D作DN⊥AB,垂足为N.
(1)如果AB=5,求BD的长;
(2)设AB=x,BD=y,求出y关于x的函数解析式,并写出x的取值范围;
(3)当AB取何值时,四边形ACDN的面积是△BDN面积的3倍?
解:(1)在直角三角形ABC中,∠ACB=90°,AC=4,AB=5,
∴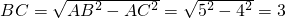 .
.
∵AD是∠CAB的平分线,且DC⊥AC,DN⊥AB,
∴DN=DC.
在Rt△DNB和Rt△ACB中,∠DBN=∠ABC,
∴△DNB∽△ACB.
∴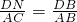 ,
,
∴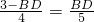 ,
,
∴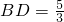 .
.
(2)在Rt△ACB中,∠ACB=90°,AC=4,AB=x,
∴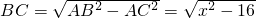 .
.
∵△DNB∽△ACB,
∴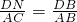 ,
,
∴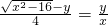 .
.
∴ .
.
(x>4).
(3)∵S四边形ACDN=3S△BDN,
∴S△ABC=4S△BDN.
又∵△ACB∽△DNB,
∴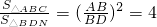 ,
,
∴AB=2BD.
设AB=x,则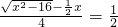 ,
,
解方程得: .
.
经检验 都是原方程的根,但x2=-4不合题意,舍去.
都是原方程的根,但x2=-4不合题意,舍去.
∴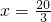 ,即
,即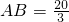 时,四边形ACDN的面积是△BDN面积的3倍.
时,四边形ACDN的面积是△BDN面积的3倍.
分析:(1)根据勾股定理可求BC;根据角平分线性质得CD=DN;根据△BDN∽△BAC得比例式求解;
(2)思路同上.
(3)四边形ACDN的面积是△BDN面积的3倍,则S△BDN= S△ABC,即两个三角形的相似比为1:2,亦即当AB=2BD时,四边形ACDN的面积是△BDN面积的3倍.
S△ABC,即两个三角形的相似比为1:2,亦即当AB=2BD时,四边形ACDN的面积是△BDN面积的3倍.
点评:此题考查相似三角形的判定与性质、角平分线的性质、解方程等知识点,综合性强,难度大.
∴
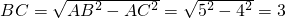 .
.∵AD是∠CAB的平分线,且DC⊥AC,DN⊥AB,
∴DN=DC.
在Rt△DNB和Rt△ACB中,∠DBN=∠ABC,
∴△DNB∽△ACB.
∴
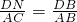 ,
,∴
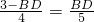 ,
,∴
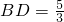 .
.(2)在Rt△ACB中,∠ACB=90°,AC=4,AB=x,
∴
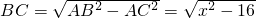 .
.∵△DNB∽△ACB,
∴
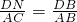 ,
,∴
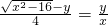 .
.∴
 .
.(x>4).
(3)∵S四边形ACDN=3S△BDN,
∴S△ABC=4S△BDN.
又∵△ACB∽△DNB,
∴
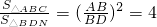 ,
,∴AB=2BD.
设AB=x,则
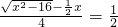 ,
,解方程得:
 .
.经检验
 都是原方程的根,但x2=-4不合题意,舍去.
都是原方程的根,但x2=-4不合题意,舍去.∴
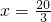 ,即
,即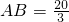 时,四边形ACDN的面积是△BDN面积的3倍.
时,四边形ACDN的面积是△BDN面积的3倍.分析:(1)根据勾股定理可求BC;根据角平分线性质得CD=DN;根据△BDN∽△BAC得比例式求解;
(2)思路同上.
(3)四边形ACDN的面积是△BDN面积的3倍,则S△BDN=
 S△ABC,即两个三角形的相似比为1:2,亦即当AB=2BD时,四边形ACDN的面积是△BDN面积的3倍.
S△ABC,即两个三角形的相似比为1:2,亦即当AB=2BD时,四边形ACDN的面积是△BDN面积的3倍.点评:此题考查相似三角形的判定与性质、角平分线的性质、解方程等知识点,综合性强,难度大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 AD与射线CM交于点D,过点D作DN⊥AB,垂足为N.
AD与射线CM交于点D,过点D作DN⊥AB,垂足为N. 如图,已知AC⊥BD于点O,AB=AD=BC=8cm,则DC=________cm.
如图,已知AC⊥BD于点O,AB=AD=BC=8cm,则DC=________cm.
