题目内容
点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.
(1)求证:点A是DO的中点.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=
 ,求△ACF的面积.
,求△ACF的面积.
(1)见解析(2)18解析:
(1)连接OB,∵ BD是⊙O的切线,
∴∠OBD=90°,
∵AB=AD,
∴∠D=∠ABD,
∴∠AOB=∠ABO,
∴AB=AO,
∵AB=AD.
∴AO=AD…………………5分
(2)∵AC是直径,∴∠ABF=90°,
∴cos∠BFA= ,…………………7分
,…………………7分
∵∠E=∠C, ∠FAC=∠FBE,
∴△FAC∽△FBE,…………………9分
∴
∵
∴△FAC的面积为18. …………………11分
(1)连接OB,求得∠AOB=∠ABO,从而求得AO=AD
(2)同弧所对的圆周角相等,可证明△ACF∽△BEF,得出一相似比,再利用三角形的面积比等于相似比的平方即可求解
(1)连接OB,∵ BD是⊙O的切线,
∴∠OBD=90°,
∵AB=AD,
∴∠D=∠ABD,
∴∠AOB=∠ABO,
∴AB=AO,
∵AB=AD.
∴AO=AD…………………5分
(2)∵AC是直径,∴∠ABF=90°,
∴cos∠BFA=
 ,…………………7分
,…………………7分∵∠E=∠C, ∠FAC=∠FBE,
∴△FAC∽△FBE,…………………9分
∴

∵

∴△FAC的面积为18. …………………11分
(1)连接OB,求得∠AOB=∠ABO,从而求得AO=AD
(2)同弧所对的圆周角相等,可证明△ACF∽△BEF,得出一相似比,再利用三角形的面积比等于相似比的平方即可求解

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.
已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.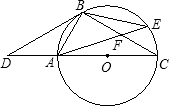 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分. 点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.
点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.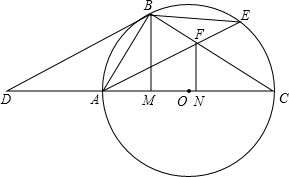 =30°.
=30°.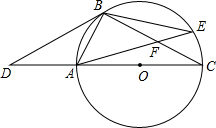 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.