题目内容
 点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.
点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.(1)求证:点A是DO的中点.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=
| 2 | 3 |
分析:(1)连接OB,利用切线的性质和已知条件证明AO=AD即可;
(2)同弧所对的圆周角相等,可证明△ACF∽△BEF,得出一相似比,再利用三角形的面积比等于相似比的平方即可求解.
(2)同弧所对的圆周角相等,可证明△ACF∽△BEF,得出一相似比,再利用三角形的面积比等于相似比的平方即可求解.
解答:证明:(1)连接OB,∵BD是⊙O的切线,
∴∠OBD=90°,
∵AB=AD,
∴∠D=∠ABD,
∴∠AOB=∠ABO,
∴AB=AO,
∴AO=AD,
∴点A是DO的中点;
(2)∵AC是直径,
∴∠ABF=90°,
cos∠BFA=
=
,
∵∠E=∠C,∠FAC=∠FBE,
∴△FAC∽△FBE,
∴
=
,
∵△BEF的面积为8,
∴△FAC的面积为18.

∴∠OBD=90°,
∵AB=AD,
∴∠D=∠ABD,
∴∠AOB=∠ABO,
∴AB=AO,
∴AO=AD,
∴点A是DO的中点;
(2)∵AC是直径,
∴∠ABF=90°,
cos∠BFA=
| FB |
| FA |
| 2 |
| 3 |
∵∠E=∠C,∠FAC=∠FBE,
∴△FAC∽△FBE,
∴
| S△BEF |
| SACF |
| 4 |
| 9 |
∵△BEF的面积为8,
∴△FAC的面积为18.
点评:本题综合考查了圆的切线的性质、圆的性质、相似三角形的判定及性质等内容,是一个综合较强的题目,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.
已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.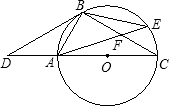 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.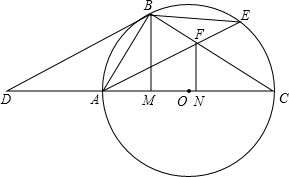 =30°.
=30°.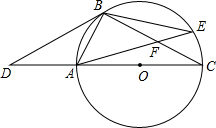 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.