题目内容
由m(a+b+c)=ma+mb+mc,可得:(a+b)(a2-ab+b2)=a3-a2b+ab2+a2b-ab2+b3=a3+b3,即(a+b)(a2-ab+b2)=a3+b3--①.我们把等式①叫做多项式乘法的立方公式.下列应用这个立方公式进行的变形正确的是( )
分析:根据多项式乘法的立方公式分别计算各选项的左边,再与右边比较即可.
解答:解:A、∵(a+1)(a2-a+1)=a3+1,∴(a+1)(a2+a+1)≠a3+1,故本选项错误;
B、(x+3)(x2-3x+9)=x3+27,故本选项错误;
C、(x+4y)(x2-4x•y+16y2)=x3+64y3,故本选项正确;
D、(2x+y)(4x2-2xy+y2)=8x3+y3,故本选项错误.
故选C.
B、(x+3)(x2-3x+9)=x3+27,故本选项错误;
C、(x+4y)(x2-4x•y+16y2)=x3+64y3,故本选项正确;
D、(2x+y)(4x2-2xy+y2)=8x3+y3,故本选项错误.
故选C.
点评:本题主要考查学生的阅读理解能力及多项式乘法的立方公式,透彻理解公式是解题的关键.

练习册系列答案
相关题目

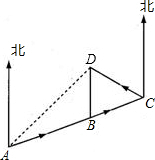 一列火车由A市途经B、C两市到达D市.如图,其中A、B、C三市在同一直线上,D市在A市的北偏东45°方向,在B市的正北方向,在C市的北偏西60°方向,C市在A市的北偏东75°方向.已知B、D两市相距100km.问该火车从A市到D市共行驶了多少路程?(参考数据:
一列火车由A市途经B、C两市到达D市.如图,其中A、B、C三市在同一直线上,D市在A市的北偏东45°方向,在B市的正北方向,在C市的北偏西60°方向,C市在A市的北偏东75°方向.已知B、D两市相距100km.问该火车从A市到D市共行驶了多少路程?(参考数据: