Question

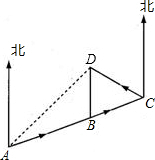一列火车由A市途经B、C两市到达D市．如图，其中A、B、C三市在同一直线上，D市在A市的北偏东45°方向，在B市的正北方向，在C市的北偏西60°方向，C市在A市的北偏东75°方向．已知B、D两市相距100km．问该火车从A市到D市共行驶了多少路程？（参考数据：

2

≈1.4，

3

≈1.7）

Answer 1

分析：本题为了求A市到D市共行驶的路程，即AB+BC+CD，可作BE⊥CD于E，BF⊥AD于F，由方向角及BD的长求出各段的长，再相加求和即可．

解答：解：过点B分别作BE⊥CD于E，BF⊥AD于F．
由题，∠BDE=60°，∠BCE=45°，∠BDF=45°，∠BAF=30°．
∴DE=50，BE=50

3

，CE=50

3

．
∴BC=50

6

．∵BF=50

2

．
∴AB=100

2

．
∴AB+BC+CD=100

2

+50

6

+50

3

+50=394km．
∴该火车从A市到D市共行驶了394km．

点评：本题主要考查了方向角的含义，正确记忆三角函数的定义是解决本题的关键．