题目内容
 如图,⊙O的直径CD垂直于弦AB,垂足为点P,若AP=6cm,PD=4cm,则⊙O的直径为________ cm.
如图,⊙O的直径CD垂直于弦AB,垂足为点P,若AP=6cm,PD=4cm,则⊙O的直径为________ cm.
13
分析:作辅助线OA(如图,连接OA)构建直角三角形AOP,在直角三角形中利用勾股定理即可求得圆O的半径OA的长度;然后根据圆的直径与半径间的数量关系来求该圆的直径的长度.
解答: 解:如图,连接OA.
解:如图,连接OA.
∵OA=OD(⊙O的半径),OP+PD=OD,PD=4cm,
∴OP=OA-4cm;
∵⊙O的直径CD垂直于弦AB,
∴∠APO=90°,
∴OA2=AP2+OP2,即OA2=(6cm)2+(OA-4cm)2,
∴OA= cm,
cm,
∴⊙O的直径为:2OA=13cm.
故答案是:13.
点评:本题考查了勾股定理和垂径定理的知识,解题的关键是利用垂径定理和相交弦定理求线段的长.
分析:作辅助线OA(如图,连接OA)构建直角三角形AOP,在直角三角形中利用勾股定理即可求得圆O的半径OA的长度;然后根据圆的直径与半径间的数量关系来求该圆的直径的长度.
解答:
 解:如图,连接OA.
解:如图,连接OA.∵OA=OD(⊙O的半径),OP+PD=OD,PD=4cm,
∴OP=OA-4cm;
∵⊙O的直径CD垂直于弦AB,
∴∠APO=90°,
∴OA2=AP2+OP2,即OA2=(6cm)2+(OA-4cm)2,
∴OA=
 cm,
cm,∴⊙O的直径为:2OA=13cm.
故答案是:13.
点评:本题考查了勾股定理和垂径定理的知识,解题的关键是利用垂径定理和相交弦定理求线段的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )| A、80° | B、50° | C、40° | D、20° |
 如图,⊙O的直径CD过弦EF的中点G,∠OEF=34°,则∠DCF的度数是
如图,⊙O的直径CD过弦EF的中点G,∠OEF=34°,则∠DCF的度数是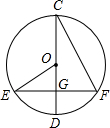 如图,⊙O的直径CD过弦EF的中点G,∠EOG=60°,则∠DCF的度数为
如图,⊙O的直径CD过弦EF的中点G,∠EOG=60°,则∠DCF的度数为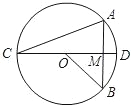 如图,⊙O的直径CD过弦AB的中点M,∠ACD=28°,则∠B=
如图,⊙O的直径CD过弦AB的中点M,∠ACD=28°,则∠B=