Question

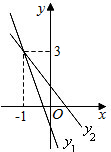已知直线y₁=mx+n和y₂=ax+b在平面直角坐标系中的位置如图所示，不等式mx+n≤ax+b的解集是

1. A.

   x≥3

2. B.

   x≤3

3. C.

   x≥-1

4. D.

   x≤-1

Answer 1

C
分析：由图象可以知道，当x=-1时，两个函数的函数值是相等的，再根据函数的增减性可以判断出不等式mx+n≤ax+b的解集．
解答：两个条直线的交点坐标为（-1，3），
当x＜-1时，
直线y₁在直线y₂的上方，
当x＞-1时，
直线y₁在直线y₂的下方，
故不等式mx+n≤ax+b的解集为x≥-1．
故选：C．
点评：本题主要考查一次函数和一元一次不等式的知识点，本题是借助一次函数的图象解一元一次不等式，两个图象的“交点”是两个函数值大小关系的“分界点”，在“分界点”处函数值的大小发生了改变，难度适中．