题目内容
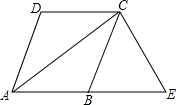 已知:AC为菱形ABCD的对角线,过C作EC⊥AC,交AB延长线于E.
已知:AC为菱形ABCD的对角线,过C作EC⊥AC,交AB延长线于E.(1)求证:CD=
| 1 |
| 2 |
(2)若四边形ADCE为等腰梯形,AC=
| 6 |
考点:菱形的性质,等腰梯形的性质
专题:
分析:(1)利用菱形的性质得出EC∥BF,再利用平行线分线段成比例定理得出AB=BE,则AB=BE=CD进而得出答案;
(2)利用等腰梯形以及菱形的性质得出CE=
AE,进而利用勾股定理得出CM的长,再利用梯形面积求法得出即可.
(2)利用等腰梯形以及菱形的性质得出CE=
| 1 |
| 2 |
解答:(1)证明:连接BD,
∵AC、BD为菱形ABCD的对角线,
∴AC⊥BD,AF=CF,AB=BC,
∵EC⊥AC,
∴EC∥BF,
∴AB=BE,
∴AB=BE=CD,
∴CD=
AE;
(2)解:过点C作CM⊥AE于点M,
∵四边形ADCE为等腰梯形,
∴AD=EC,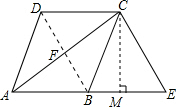
∵CD=
AE,CE=AD=CD,
∴CE=
AE,
设CE=x,则AE=2x,
∵AC=
,
∴x2+(
)2=(2x)2,
解得:x=±
(负数舍去),
∴CM×AE=AC×EC,
∴2
CM=
×
,
解得:CM=
,
∴四边形ADCE的面积为:
(CD+AE)×CM=
(
+2
)×
=
.
∵AC、BD为菱形ABCD的对角线,
∴AC⊥BD,AF=CF,AB=BC,
∵EC⊥AC,
∴EC∥BF,
∴AB=BE,
∴AB=BE=CD,
∴CD=
| 1 |
| 2 |
(2)解:过点C作CM⊥AE于点M,
∵四边形ADCE为等腰梯形,
∴AD=EC,

∵CD=
| 1 |
| 2 |
∴CE=
| 1 |
| 2 |
设CE=x,则AE=2x,
∵AC=
| 6 |
∴x2+(
| 6 |
解得:x=±
| 2 |
∴CM×AE=AC×EC,
∴2
| 2 |
| 6 |
| 2 |
解得:CM=
| ||
| 2 |
∴四边形ADCE的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
点评:此题主要考查了菱形的性质以及勾股定理和梯形面积公式等知识,根据已知得出CE=
AE是解题关键.
| 1 |
| 2 |

练习册系列答案
相关题目
在0、-3.14、π、0.212112111211112…(每两个2之间的1依次增加)、-
、
,这6个数中,有理数的个数为( )
| • |
| 3 |
| 22 |
| 7 |
| A、5个 | B、4个 | C、3个 | D、2个 |
用配方法解方程2x2+1=3x,配方正确的是( )
A、(x-
| ||||
B、(x-
| ||||
C、(x-
| ||||
D、(x+
|