题目内容
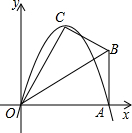
 已知如图,梯形OABC的底边OC在x轴上,AB∥OC,BC⊥CO,过点A的双曲线y=
已知如图,梯形OABC的底边OC在x轴上,AB∥OC,BC⊥CO,过点A的双曲线y=| k |
| x |
分析:延长BA交y轴于E,过P作x轴的垂线,垂足为F,根据三角形的面积公式得出△OCB的面积=△OBE的面积,根据反比例函数系数k的几何意义得出△OPF的面积=△OAE的面积,则梯形PFCB的面积=△OAB的面积,再根据相似三角形的性质得出△OPF的面积=
梯形PFCB的面积,则
k=
,进而求出k的值.
| 1 |
| 15 |
| 1 |
| 2 |
| 1 |
| 5 |
解答: 解:延长BA交y轴于E,过P作x轴的垂线,垂足为F.
解:延长BA交y轴于E,过P作x轴的垂线,垂足为F.
由△OCB的面积=△OBE的面积,△OPF的面积=△OAE的面积,
∵OP:PB=1:3,
∴OP:OB=1:4,
∴△OPF的面积=
梯形PFCB的面积=
△OAB的面积=
×3=
,
即
k=
,
k=
.
故选A.
 解:延长BA交y轴于E,过P作x轴的垂线,垂足为F.
解:延长BA交y轴于E,过P作x轴的垂线,垂足为F.由△OCB的面积=△OBE的面积,△OPF的面积=△OAE的面积,
∵OP:PB=1:3,
∴OP:OB=1:4,
∴△OPF的面积=
| 1 |
| 15 |
| 1 |
| 15 |
| 1 |
| 15 |
| 1 |
| 5 |
即
| 1 |
| 2 |
| 1 |
| 5 |
k=
| 2 |
| 5 |
故选A.
点评:本题考查了反比例系数k的几何意义.此题还可这样理解:当满足OP:PB=1:3时,点P在函数图象上运动,面积为定值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
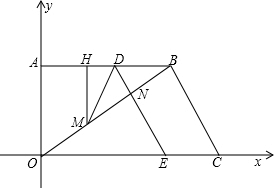
 .问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. 移动的时间是秒t,设△OPD的面积是S.
移动的时间是秒t,设△OPD的面积是S.