题目内容
已知在直角梯形ABCD中,AD∥BC,CD⊥BC,将其沿对角线BD折叠,点A恰好落在边CD所在的直线上的点A′,若AB=13,BC=12,则AD的长为 .
【答案】分析:先画出图形,过点A作AE⊥BC于点E,在Rt△A′BC中求出A′C,设AD=x,则CD=x+5,在Rt△AEB中,利用勾股定理可得出关于x的方程,解出即可.
解答:解:过点A作AE⊥BC于点E,则A′B=AB=13,

在Rt△A′BC中,A′C= =5,
=5,
设AD=x,则CD=A′D+A′C=x+5,
在Rt△ABE中,BE2+AE2=AB2,即(12-x)2+(x+5)2=132,
解得:x=7,即AD=7.
故答案为:7.
点评:本题考查了翻折变换及梯形的知识,解答本题的关键是熟练掌握翻折变换的性质及勾股定理的表达式,难度一般.
解答:解:过点A作AE⊥BC于点E,则A′B=AB=13,

在Rt△A′BC中,A′C=
 =5,
=5,设AD=x,则CD=A′D+A′C=x+5,
在Rt△ABE中,BE2+AE2=AB2,即(12-x)2+(x+5)2=132,
解得:x=7,即AD=7.
故答案为:7.
点评:本题考查了翻折变换及梯形的知识,解答本题的关键是熟练掌握翻折变换的性质及勾股定理的表达式,难度一般.

练习册系列答案
相关题目
 已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.
已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.
 26、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知∵,G为CH的中点.
26、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知∵,G为CH的中点.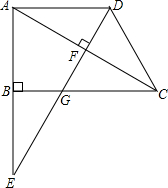 (2012•李沧区一模)已知:如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.
(2012•李沧区一模)已知:如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.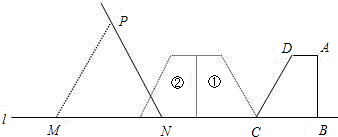 与等边三角形重叠部分的面积等于直角梯形ABCD的面积的一半,这时等边三角形的边长应为多少?
与等边三角形重叠部分的面积等于直角梯形ABCD的面积的一半,这时等边三角形的边长应为多少?