题目内容
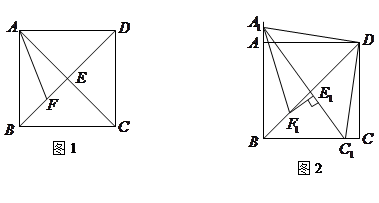
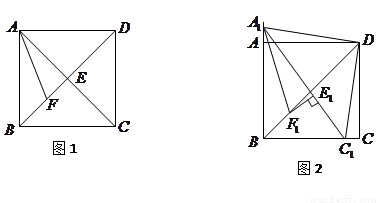
如图1,在正方形![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求证:![]() ;
;
(2)在图1中,若![]() 在
在![]() 上,且
上,且![]() ,则
,则![]() 成立吗?为什么?
成立吗?为什么?
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题:
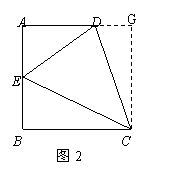
①如图2,在直角梯形ABCD中,![]() ∥
∥![]()
![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,且∠DCE=45°,求DE的长;
的中点,且∠DCE=45°,求DE的长;
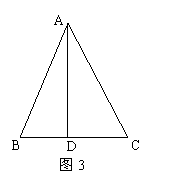
②如图3,在△ABC中,∠BAC=45°,AD⊥BC,![]() ,则
,则
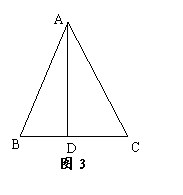

![]() 的面积为 (直接写出结果,不需要写出计算过程).
的面积为 (直接写出结果,不需要写出计算过程).
 |
证明:(1)在正方形ABCD中
 CB=CD, ∠B=∠CDA=90°
CB=CD, ∠B=∠CDA=90°
∴∠CDF=∠B =90°
∵DF=BE
∴△BCE≌△DCF(SAS)
∴CE=CF
(2)GE=BE+GD成立
理由:∵∠BCD=90°∠GCE=45°
∴∠BCE+∠GCD=45°
∵△BCE≌△DCF(已证)
∴∠BCE=∠DCF
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=45°
 ∴∠ECG=∠FCG=45°
∴∠ECG=∠FCG=45°
∵CE=CF ,CG=CG
∴△ECG≌△FCG(SAS)
∴GE=FG
∵FG=GD+DF
∴GE=BE+GD
 (3)①
(3)①
解:过点C作CG⊥AD交AD的延长线于点G,
由(1)和题设知 DE=DG+BE.
设DG=x,则AD=12-x,DE=x+6,
在Rt△ADE中,AD2+AE2=DE2
∴ 62+(12-x)2=(x+6)2 解得 x=4.
∴DE=6+4=10.
② 15.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
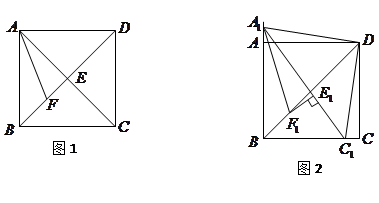
 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
, 平分
平分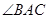 ,交
,交 .
.
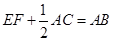 ;
; 从点
从点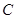 出发,沿着线段
出发,沿着线段 向点
向点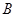 运动(不与点
运动(不与点 从点
从点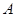 出发,沿着
出发,沿着 的延长线运动,点
的延长线运动,点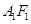 平分
平分 ,交
,交 ,过点
,过点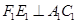 ,垂足为
,垂足为 ,请猜想
,请猜想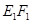 ,
,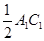 与
与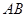 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想; ,
,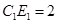 时,求
时,求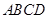 中,点
中,点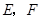 分别为边
分别为边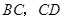 的中点,
的中点,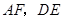 相交于点
相交于点 ,则可得结论:①
,则可得结论:①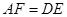 ;②
;②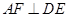 .(不需要证明)
.(不需要证明)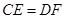 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”) 的延长线和
的延长线和 的延长线上,且
的延长线上,且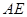 和
和 ,若点
,若点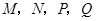 分别为
分别为 的中点,请判断四边形
的中点,请判断四边形 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.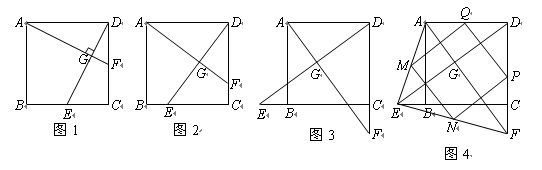
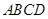 中,对角线
中,对角线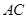 与
与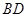 相交于点
相交于点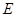 ,
,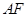 平分
平分 ,交
,交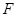 .
. ;
;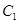 从点
从点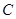 出发,沿着线段
出发,沿着线段 向点
向点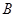 运动(不与点
运动(不与点 从点
从点 出发,沿着
出发,沿着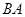 的延长线运动,点
的延长线运动,点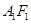 平分
平分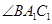 ,交
,交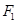 ,过点
,过点 ,垂足为
,垂足为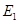 ,请猜想
,请猜想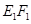 ,
,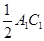 与
与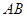 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想; ,
, 时,求
时,求
 中,对角线
中,对角线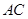 与
与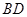 相交于点
相交于点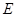 ,
, 平分
平分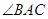 ,交
,交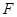 .
.
 ;
;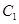 从点
从点 出发,沿着线段
出发,沿着线段 向点
向点 运动(不与点
运动(不与点 从点
从点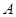 出发,沿着
出发,沿着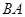 的延长线运动,点
的延长线运动,点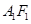 平分
平分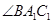 ,交
,交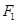 ,过点
,过点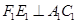 ,垂足为
,垂足为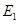 ,请猜想
,请猜想 ,
,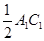 与
与 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想; ,
, 时,求
时,求