题目内容
实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
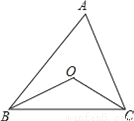
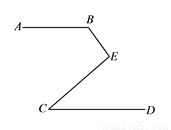
(1)如图,一束光线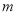 射到平面镜
射到平面镜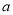 上,被
上,被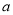 反射到平面镜
反射到平面镜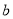 上,又被
上,又被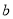 反射,若被
反射,若被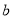 反射出的光线
反射出的光线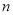 与光线
与光线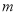 平行,且
平行,且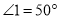 ,则
,则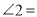 _________,
_________, 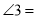 ________.
________.
(2)在(1)中,若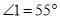 ,则
,则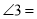 _______;若
_______;若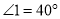 ,则
,则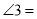 ________;
________;
(3)由(1)、(2),请你猜想:当两平面镜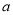 、
、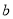 的夹角
的夹角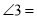 ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜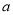 上的光线
上的光线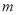 ,经过平面镜
,经过平面镜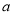 、
、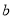 的两次反射后,入射光线
的两次反射后,入射光线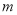 与反射光线
与反射光线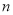 平行.请说明理由.
平行.请说明理由.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若分式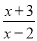 有意义,则
有意义,则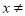 _____.
_____.
 2
【解析】根据分式的分母不等于0时,分式有意义,列出不等式即可得出答案.
【解析】
因为分式有意义,
所以,
解得,
故答案为: .
2
【解析】根据分式的分母不等于0时,分式有意义,列出不等式即可得出答案.
【解析】
因为分式有意义,
所以,
解得,
故答案为: . 计算: 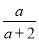 -
-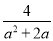 =_____.
=_____.
 【解析】因为-=-=,故答案为: .
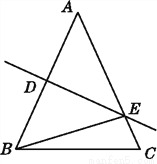
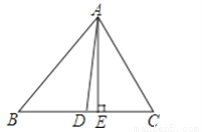
【解析】因为-=-=,故答案为: . 如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
 8
【解析】试题分析:由DE是△ABE的对称轴,根据轴对称的性质可得AE=BE,再由C△BCE=BC+CE+BE=14,可得BC+AC=14,从而求得AB的长.
试题解析:
因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8.
8
【解析】试题分析:由DE是△ABE的对称轴,根据轴对称的性质可得AE=BE,再由C△BCE=BC+CE+BE=14,可得BC+AC=14,从而求得AB的长.
试题解析:
因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8. 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
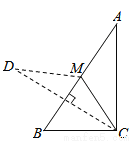
A.30° B.40° C.50° D.60°
 A.
【解析】
试题解析:如图,
∵CM是斜边AB上的中线,
∴CM=AM=AB,
∴∠A=∠MCA(设为α);
由翻折变换的性质得:∠DCM=∠MCA=α;
∵CD⊥AB,
∴∠DCA+∠A=90°,
即3α=90°,
∴∠A=α=30°.
故选A.
A.
【解析】
试题解析:如图,
∵CM是斜边AB上的中线,
∴CM=AM=AB,
∴∠A=∠MCA(设为α);
由翻折变换的性质得:∠DCM=∠MCA=α;
∵CD⊥AB,
∴∠DCA+∠A=90°,
即3α=90°,
∴∠A=α=30°.
故选A. 

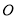 点的灯泡发出的两束光线
点的灯泡发出的两束光线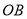 、
、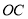 经灯碗反射后平行射出,如果图中
经灯碗反射后平行射出,如果图中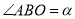 ,
, 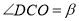 ,则
,则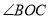 的度数为( ).
的度数为( ).
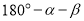 B.
B. 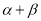 C.
C.  D.
D. 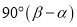
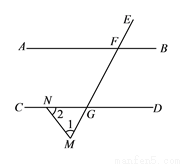
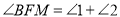 ,求证:
,求证: 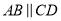 .
.
 ,
,  ,
,  ,则
,则 __________.
__________.
 ∠BAC=35°.
∠BAC=35°.