题目内容
11.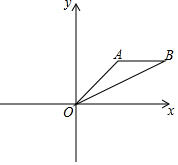 如图,△ABO中,点O是坐标原点,A(2,2),B(4,2),点C在x轴正半轴上,O,B,C三点所构成的三角形与△ABO相似,则点C的坐标是(2,0)或(10,0).
如图,△ABO中,点O是坐标原点,A(2,2),B(4,2),点C在x轴正半轴上,O,B,C三点所构成的三角形与△ABO相似,则点C的坐标是(2,0)或(10,0).
分析 分两种情形讨论即可①△BOC∽△OBA.②△BOC′∽△OBA分别计算即可.
解答 解:如图,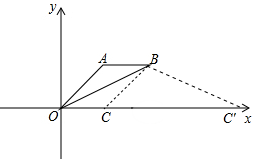
∵A(2,2),B(4,2),
∴AB∥x,AB=2,OB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
①当BC∥OA时,
∵∠AOB=∠CBO,∠ABO=∠BOC,
∴△BOC∽△OBA,
∵AB∥OC,BC∥OA,
∴四边形OABC是平行四边形,
∴OC=AB=2,
∴C(2,0).
②当△BOC′∽△OBA时,
$\frac{OC′}{OB}$=$\frac{OB}{AB}$,
∴$\frac{OC′}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{2}$,
∴OC′=10,
∴C′(10,0),
故答案为(2,0)或(10,0).
点评 本题考查相似三角形的判定和性质、坐标与图形的性质等知识,解题的关键是学会用 分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
19.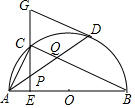 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )| A. | ①③⑤ | B. | ②④⑤ | C. | ①②⑤ | D. | ①③④ |
3.已知a-2b=3,则3(a-b)-(a+b)的值为( )
| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
1.到三角形三边距离相等的点是( )
| A. | 三角形的两条平分线的交点 | |
| B. | 三角形的两条高的交点 | |
| C. | 三角形的三条中线的交点 | |
| D. | 三角形的三条边的垂直平分线的交点 |
