题目内容
 如图,Rt△OAB的斜边AO在x轴的正半轴上,直角顶点B在第四象限内,S△OAB=20,OB:AB=1:2,求A、B两点的坐标.
如图,Rt△OAB的斜边AO在x轴的正半轴上,直角顶点B在第四象限内,S△OAB=20,OB:AB=1:2,求A、B两点的坐标.
解:∵OB:AB=1:2,
∴设OB=x,则AB=2x,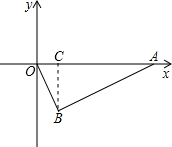
∴OA=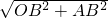 =
= x,
x,
∵S△OAB=20= OB•AB,
OB•AB,
∴20= •x•2x,
•x•2x,
∴x2=20,
∴x=2 ,
,
∴OA= ×2
×2 =10,
=10,
∴点A的坐标是(10,0);
过点B作BC⊥OA交OA于C,
∵S△AOB= AO•BC=20,
AO•BC=20,
∴BC=4,
∵B在第四象限,
∴B的纵坐标为-4,
∵OB=2 ,BC=4,
,BC=4,
∴OC= =2,
=2,
∴B的横坐标是2,
∴B的坐标为(2,-4).
分析:因为OB:AB=1:2,∠OBA为直角,可设OB=x,则AB=2x,OA= x,因为S△OAB=20=
x,因为S△OAB=20= OB•AB,从而求出x的值,进而得到A点的坐标,过点B作BC⊥OA交OA于C,利用三角形OBA的面积求出OA边上的高,利用勾股定理再求出OC的长即可求出B的坐标.
OB•AB,从而求出x的值,进而得到A点的坐标,过点B作BC⊥OA交OA于C,利用三角形OBA的面积求出OA边上的高,利用勾股定理再求出OC的长即可求出B的坐标.
点评:本题考查了直角三角形的面积公式、勾股定理的运用以及求点的坐标,题目难度不大,但设计比较新颖.
∴设OB=x,则AB=2x,

∴OA=
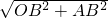 =
= x,
x,∵S△OAB=20=
 OB•AB,
OB•AB,∴20=
 •x•2x,
•x•2x,∴x2=20,
∴x=2
 ,
,∴OA=
 ×2
×2 =10,
=10,∴点A的坐标是(10,0);
过点B作BC⊥OA交OA于C,
∵S△AOB=
 AO•BC=20,
AO•BC=20,∴BC=4,
∵B在第四象限,
∴B的纵坐标为-4,
∵OB=2
 ,BC=4,
,BC=4,∴OC=
 =2,
=2,∴B的横坐标是2,
∴B的坐标为(2,-4).
分析:因为OB:AB=1:2,∠OBA为直角,可设OB=x,则AB=2x,OA=
 x,因为S△OAB=20=
x,因为S△OAB=20= OB•AB,从而求出x的值,进而得到A点的坐标,过点B作BC⊥OA交OA于C,利用三角形OBA的面积求出OA边上的高,利用勾股定理再求出OC的长即可求出B的坐标.
OB•AB,从而求出x的值,进而得到A点的坐标,过点B作BC⊥OA交OA于C,利用三角形OBA的面积求出OA边上的高,利用勾股定理再求出OC的长即可求出B的坐标.点评:本题考查了直角三角形的面积公式、勾股定理的运用以及求点的坐标,题目难度不大,但设计比较新颖.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 14、如图,Rt△OAB的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△OAB绕点O按顺时针方向旋转90°,则点B的对应点B′的坐标是
14、如图,Rt△OAB的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△OAB绕点O按顺时针方向旋转90°,则点B的对应点B′的坐标是 A(10,0),△OAB的面积为20.
A(10,0),△OAB的面积为20. (2012•阜宁县一模)如图,Rt△OAB的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△OAB绕点O按逆时针方向旋转90°,则点B的对应点的坐标为
(2012•阜宁县一模)如图,Rt△OAB的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△OAB绕点O按逆时针方向旋转90°,则点B的对应点的坐标为 (2013•海宁市模拟)如图,Rt△OAB的斜边OA在x轴上,点B在第一象限,OA:OB=5:4.边AB的垂直平分线分别交AB、x轴于点C、D,线段CD交反比例函数y=
(2013•海宁市模拟)如图,Rt△OAB的斜边OA在x轴上,点B在第一象限,OA:OB=5:4.边AB的垂直平分线分别交AB、x轴于点C、D,线段CD交反比例函数y= (2013•淄博)如图,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
(2013•淄博)如图,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )