Question

【题目】如图，已知A（0，4），B（﹣2，2），C（3，0）．

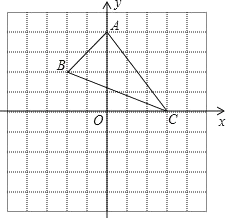
（1）作△ABC关于x轴对称的△A1B1C1；

（2）△A1B1C1的面积＝　 　．A1C1边上的高＝　 　；

（3）在x轴上有一点P，使PA+PB最小，此时PA+PB的最小值＝　 　．

Answer 1

【答案】（1）详见解析；（2）7，；（3）2

【解析】

（1）依据轴对称的性质，即可作△ABC关于x轴对称的△A1B1C1；

（2）依据割补法即可得到△A1B1C1的面积，进而得出A1C1边上的高；

（3）连接AB1，交x轴于点P，则BP＝B1P，PA+PB的最小值等于AB1的长，运用勾股定理即可得到结论．

解：（1）如图所示，△A1B1C1即为所求；

（2）△A1B1C1的面积＝4×5﹣×2×2﹣×3×4﹣×2×5＝20﹣2﹣6﹣5＝7．

∵A1C1＝＝5，

∴A1C1边上的高＝＝；

故答案为：7，；

（3）如图所示，连接AB1，交x轴于点P，则BP＝B1P，

∴PA+PB的最小值等于AB1的长，

∵AB1＝＝2，

∴PA+PB的最小值等于2，

故答案为：2．