题目内容
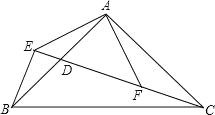
【题目】如图，一张三角形纸片ABC，其中∠BAC=60°，BC=6，点D是BC边上一动点，将BD，CD翻折使得B′，C′分别落在AB，AC边上，（B与B′，C与C′分别对应），点D从点B运动至点C，△B′C′D面积的大小变化情况是（ ）
A. 一直减小 B. 一直不变 C. 先减小后增大 D. 先增大后减小
【答案】D
【解析】
作B′H⊥DC′于H．设BD=DB′=x，则CD=DC′=6﹣x．由折叠得性质可求出∠B′DC′=60°，从而利用锐角三角函数知识表示出B′H的值，然后根据三角形的面积公式列出函数关系式解答即可.
如图，作B′H⊥DC′于H．设BD=DB′=x，则CD=DC′=6﹣x．
∵∠A=60°，
∴∠B+∠C=120°，
由翻折不变性可知：∠B=∠DB′B，∠C=∠DC′C，
∴∠BDB′+∠CDC′=120°，
∴∠B′DC′=60°，
∴B′H=sin60x=
x，
∴S△DB′C′=
x（6﹣x）=﹣
（x﹣3）2+
，
∴S△DB′C′的值先增大后减小，
故选：D．
练习册系列答案
相关题目
