题目内容
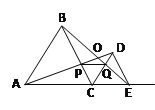
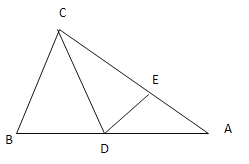
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折后,点
翻折后,点![]() 恰好落在边
恰好落在边![]() 的
的![]() 点处若
点处若![]() ,
,![]() ,则点
,则点![]() 到
到![]() 的距离是( )
的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
过点D作DF⊥BC于F,DG⊥AC于G,根据折叠的性质可得CB=CE,∠BCD=∠ACD,然后根据角平分线的性质可得DF=DG,然后结合已知条件和三角形面积公式即可求出AC和CB,然后利用S△BCD+S△ACD=![]() 列出方程即可求出DG.
列出方程即可求出DG.
解:过点D作DF⊥BC于F,DG⊥AC于G

由折叠的性质可得:CB=CE,∠BCD=∠ACD
∴CD平分∠BCA
∴DF=DG
∵![]()
∴CE:AC=5:8
∴CB:AC=5:8
即CB=![]()
∵![]()
∴![]()
解得:AC=8
∴CB=![]()
∵S△BCD+S△ACD=![]()
∴![]()
即![]()
解得:DG=![]() ,即点
,即点![]() 到
到![]() 的距离是
的距离是![]()
故选A.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目