题目内容
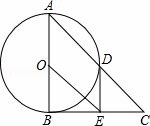
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求sin∠F.

(1)证明:连接OB.
∵CD是直径,
∴∠CBD=90°,
又∵OB=OD,
∴∠OBD=∠D,
又∠CBF=∠D,
∴∠CBF=∠OBD,
∴∠OBF=90°,即OB⊥BF,
∴FB是圆的切线;
(2)解:∵CD是圆的直径,CD⊥AB,
∴BE=AB=4,
设圆的半径是R,在 直角△OEB中,根据勾股定理得:R2=(R﹣2)2+42,
直角△OEB中,根据勾股定理得:R2=(R﹣2)2+42,
解得:R=5,
∵∠BOE=∠FOB,∠BEO=∠OBF,
∴△OBE∽△OBF,
∴OB2=OE•OF,
∴OF= =
= ,
,
则在直角△OBF中,sinF= =
= =.
=.


练习册系列答案
相关题目
下列几何体中,同一个几何体的主视图与俯视图不同的是( )
|
| A. |
圆柱 | B. |
正方体 | C. |
圆锥 | D. |
球 |
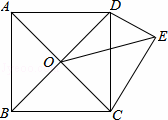
如图,ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,∠DCE=30°,若OE=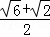 ,则正方形的面积为( )
,则正方形的面积为( )
|
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
将数据37000用科学记数法表示为3.7×10n,则n的值为( )
|
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |





 ÷(﹣),其中x=
÷(﹣),其中x= +1,y=
+1,y=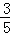 ,BE=
,BE=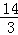 ,求OE的长.
,求OE的长.