题目内容
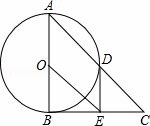
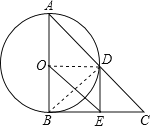
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD•OE;
(3)若cos∠BAD=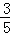 ,BE=
,BE=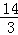 ,求OE的长.
,求OE的长.
(1)证明:连接OD,BD,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE=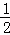 BC,
BC,
∴∠C=∠CDE,
∵OA=OD,∴∠A=∠ADO,
∵∠ABC=90°,即∠C+∠A=90°,
∴∠ADO+∠CDE=90°,即∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为圆O的切线;
(2)证明:∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴ ,即BC2=AC•CD.
,即BC2=AC•CD.
∴BC2=2CD•OE;
(3)解:∵cos∠BAD=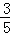 ,
,
∴sin∠BAC= =
= ,
,
又∵BE=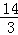 ,E是BC的中点,即BC=
,E是BC的中点,即BC=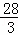 ,
,
∴AC= .
.
又∵AC=2OE,
∴OE=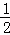 AC=
AC= .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )

|
| A. | 逐渐增大 | B. | 不变 | C. | 逐渐减小 | D. | 先增大后减小 |
已知a>b>0,下列结论错误的是( )
|
| A. | a+m>b+m | B. |
| C. | ﹣2a>﹣2b | D. |
|
如图是某个几何体的三视图,该几何体是( )

|
| A. | 长方体 | B. | 三棱柱 | C. | 正方体 | D. | 圆柱 |

 .
. =ad﹣bc,则满足等式
=ad﹣bc,则满足等式 =1的x的值为
=1的x的值为 

 (
( ﹣1)0=
﹣1)0= 