题目内容
在圣诞节前夕,几位同学到某文具店调查一种进价为2元的圣诞贺卡的销售情况,每张定价3元,每天能卖出500张,每张售价每上涨0.1元,其每天销售量就减少10个.另外,物价局规定,售价不得超过商品进价的240%.据此,请你解答下面问题:
(1)要实现每天800元的利润,应如何定价?
(2)800元的利润是否最大?如何定价,才能获得最大利润?
【考点】二次函数的应用;一元二次方程的应用.
【专题】销售问题.
【分析】(1)设要实现每天800元的利润定价为x元,由总利润=每个的利润×数量列方程即可解答;
(2)设每天的利润为y元,由总利润=每个的利润×数量就可以得出y与x的关系式,将解析式化为顶点式就可以求出结论.
【解答】解:(1)设要实现每天800元的利润定价为x元,根据题意,得
(x﹣2)(500﹣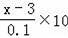
 )=800
)=800
整理得:x2﹣10x+24=0
解得:x1=4,x2=6
∵物价局规定,售价不得超过商品进价的240%.
即2×240%=4.8,
∴x2=6不合题意舍去,
∴要实现每天800元的利润,应定价每张4元;
(2)设每天的利润为y元,则
y=(x﹣2)(500﹣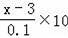
 )
)
=﹣100x2+1000x﹣1600
=﹣100(x﹣5)2+900
∵x≤5时,y随x的增大而增大,并且x≤4.8,
∴当x=4.8元时,利润最大,
y最大=﹣100(4.8﹣5)2+900=896>800,
∴800元的利润不是最大利润,当定价为4.8元时,才能获得最大利润.
【点评】本题考查了销售问题的数量关系的运用,总利润=每个的利润×数量,二次函数的解析式的运用,二次函数的性质的运用,解答时求出函数解析式是关键.

练习册系列答案
相关题目

 的解是 .
的解是 .
 ÷(a+2)+
÷(a+2)+
 ,再求值,a为整数且﹣2≤a≤2.
,再求值,a为整数且﹣2≤a≤2.


 的中点,∠ABC=50°,则∠DAB等于( )
的中点,∠ABC=50°,则∠DAB等于( )

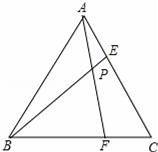

 _______°
_______°