题目内容
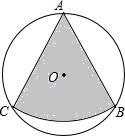已知：如图，⊙O的半径为2，AB是⊙O的一条弦，把弦AB绕点A顺时针旋转60°，点B正好与⊙O上的另一点C重合，那么弦AB所经过图形（阴影部分）的面积是（ ）| A、π | ||
| B、2π | ||
C、
| ||
| D、无法计算 |
考点：扇形面积的计算
专题：
分析：连接AO，作OD⊥AC于点D，利用含30°的直角三角形求出AD，再求出AC，利用扇形面积的计算即可．
解答：解：如图，连接AO，作OD⊥AC于点D，
∵AO=2，∠BAC=60°，
∴∠OAD=30°，
∴AD=
，
∴AC=2
，
∴弦AB所经过图形（阴影部分）的面积是
=2π．
故选：B．
∵AO=2，∠BAC=60°，
∴∠OAD=30°，
∴AD=
| 3 |
∴AC=2
| 3 |
∴弦AB所经过图形（阴影部分）的面积是
π(2
| ||
| 360° |
故选：B．
点评：本题主要考查了扇形面积的计算，解题的关键是求出AC的值．
练习册系列答案
相关题目
如图所示是一个底面为正方形的几何体，则它的俯视图可能为（ ）A、 |
B、 |
C、 |
D、 |
如图，在△ABC中，AD是BC上的高，tan∠B=cos∠DAC，下列说法中，正确的是（ ）
| A、长度相等的弧叫等弧 |
| B、直角所对的弦是直径 |
| C、同弦所对的圆周角相等 |
| D、等弧所对的弦相等 |
一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图的扇形的圆心角是（ ）
| A、120° | B、150° |
| C、180° | D、240° |