��Ŀ����
����Ŀ�����������⣩������ѧ��С��������ҵʱ����������һ����Ŀ��
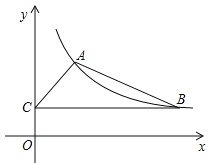
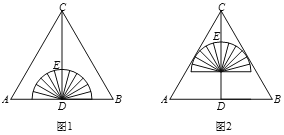
��ͼ�٣���OΪ����ԭ�㣬��O�İ뾶Ϊ1����A��2��0��������B�ڡ�O�ϣ�����AB�����ȱߡ�ABC��A��B��CΪ˳ʱ��˳����OC�����ֵ
��������⣩С��������εij�����̽�������ڵõ�����˼·����ͼ���У�����OB����OBΪ����OB��������ȱ�������BOE������AE��
��1�������ҳ�ͼ����OC��ȵ��߶Σ���˵�����ɣ�
��2�����߶�OC�����ֵ��
��������ã�
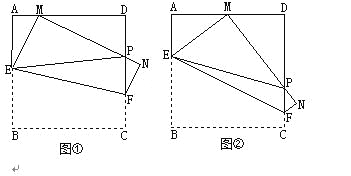
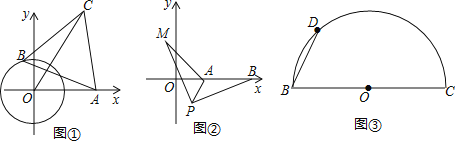
��3����ͼ�ڣ���ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��5��0������PΪ�߶�AB��һ���㣬��PA��2��PM��PB����BPM��90�㣬���߶�AM�������ֵ����ʱ��P�����꣮
��Ǩ����չ��
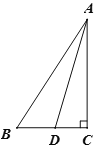
��4����ͼ�ۣ�BC��4![]() ����D����BCΪֱ���İ�Բ�ϲ�ͬ��B��C��һ�����㣬��BDΪ�����ȱߡ�ABD����ֱ��д��AC����ֵ��
����D����BCΪֱ���İ�Բ�ϲ�ͬ��B��C��һ�����㣬��BDΪ�����ȱߡ�ABD����ֱ��д��AC����ֵ��
���𰸡���1�����ۣ�OC��AE�����ɼ���������2��OC�����ֵΪ3����3�����ֵΪ2![]() +3��P��2��
+3��P��2��![]() ��
��![]() ������4��AC�����ֵΪ2
������4��AC�����ֵΪ2![]() +2
+2![]() �� 2
�� 2![]() ��2
��2![]() ��
��
��������
��1�����ۣ�![]() ��ֻҪ֤��
��ֻҪ֤��![]() ���ɣ�
���ɣ�
��2�����������ε����߹�ϵ���ɽ�����⣻
��3������![]() ����
����![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ���õ�
���õ�![]() �ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�
�ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�![]() ��
��![]() �����ݵ�
�����ݵ�![]() ���߶�
���߶�![]() ���ӳ���ʱ���߶�
���ӳ���ʱ���߶�![]() ȡ�����ֵ�����ɵõ����ֵΪ
ȡ�����ֵ�����ɵõ����ֵΪ![]() ����
����![]() ��
��![]() ����
����![]() �����ݵ���ֱ�������ε����ʣ����ɵõ����ۣ�
�����ݵ���ֱ�������ε����ʣ����ɵõ����ۣ�
��4����ͼ4�У���![]() Ϊ�����ȱ�������
Ϊ�����ȱ�������![]() ����
����![]() ���Ƴ�
���Ƴ�![]() ���Ƴ�����
���Ƴ�����![]() �����ֵ��ֻҪ���
�����ֵ��ֻҪ���![]() �����ֵ���ɣ���
�����ֵ���ɣ���![]() ��ֵ��
��ֵ��![]() ���Ƴ���
���Ƴ���![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ���˶�����ͼ���֪������
���˶�����ͼ���֪������![]() ��
��![]() �Ϸ���
�Ϸ���![]() ʱ��
ʱ��![]() ��ֵ���.
��ֵ���.
��1����ͼ���У����ۣ�OC��AE��
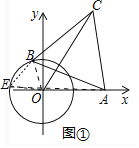
���ɣ��ߡ�ABC����BOE���ǵȱ������Σ�
��BC��BA��BO��BE����CBA����OBE��60�㣬
���CBO����ABE��
���CBO�ա�ABE��
��OC��AE��
��2���ڡ�AOE�У�AE��OE+OA��
�൱E��O��A���ߣ�
��AE�����ֵΪ3��
��OC�����ֵΪ3��
��3����ͼ1������BM��
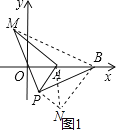
�߽���APM���ŵ�P˳ʱ����ת90��õ���PBN������AN�����APN�ǵ���ֱ�������Σ�
��PN��PA��2��BN��AM��
��A��������2��0������B��������5��0����
��OA��2��OB��5��
��AB��3��
���߶�AM�������ֵ���߶�BN�������ֵ��
�൱N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ����ͼ2�У�
���ֵ��AB+AN��
��AN��![]() AP��2
AP��2![]() ��
��
�����ֵΪ2![]() +3��
+3��
��ͼ2����P��PE��x����E��

�ߡ�APN�ǵ���ֱ�������Σ�
��PE��AE��![]() ��
��
��OE��BO��AB��AE��5��3��![]() ��2��
��2��![]() ��
��
��P��2��![]() ��
��![]() ����
����
��4����ͼ4�У���BCΪ�����ȱ������Ρ�BCM��

�ߡ�ABD����CBM��60�㣬
���ABC����DBM����AB��DB��BC��BM��
���ABC�ա�DBM��
��AC��MD��
������AC�����ֵ��ֻҪ���DM�����ֵ���ɣ�
��BC��4![]() ����ֵ����BDC��90�㣬
����ֵ����BDC��90�㣬
���D����BCΪֱ���ġ�O���˶���
��ͼ���֪������D��BC�Ϸ���DM��BCʱ��DM��ֵ������ֵ��2![]() +2
+2![]() ��
��
��AC�����ֵΪ2![]() +2
+2![]() ��
��
����A���߶�BD���Ҳ�ʱ��ͬ���ɵ�AC����СֵΪ2![]() ��2
��2![]() ��
��

 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�