题目内容
如图，在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），再把剩余的部分剪拼成一个矩形，通过计算图形（阴影部分）的面积，验证了一个等式是________．
a2-b2=（a+b）（a-b）
分析：分别表示出两个图形中的阴影部分的面积，然后根据两个阴影部分的面积相等即可得解．
解答：左边图形中，阴影部分的面积=a2-b2，
右边图形中，阴影部分的面积=（a+b）（a-b），
∵两个图形中的阴影部分的面积相等，
∴a2-b2=（a+b）（a-b）．
故答案为：a2-b2=（a+b）（a-b）．
点评：本题考查了平方差公式的几何解释，根据阴影部分的面积相等列出面积的表达式是解题的关键．
分析：分别表示出两个图形中的阴影部分的面积，然后根据两个阴影部分的面积相等即可得解．
解答：左边图形中，阴影部分的面积=a2-b2，
右边图形中，阴影部分的面积=（a+b）（a-b），
∵两个图形中的阴影部分的面积相等，
∴a2-b2=（a+b）（a-b）．
故答案为：a2-b2=（a+b）（a-b）．
点评：本题考查了平方差公式的几何解释，根据阴影部分的面积相等列出面积的表达式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
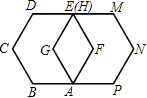如图，如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合，那么点B的对应点是点
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
如图，将边长为3的正六边形A1A2A3A4A5A6，在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为（ ）
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
长为半径作
，
，
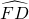，求阴影部分的面积．
长为半径作
，
，
，求阴影部分的面积．