题目内容
已知:如图,在RT△ABC中,∠ACB=90°,CA=CB, O是AB的中点,点D在BA的延长线上,以D为直角顶点作RT△DEF, FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断段OM、ON的数量关系与位置关系,并写出证明过程.

解:OM=ON,OM⊥ON.理由如下:
连接CO,则CO是AB边上的中线.
∵∠ACB=90°,∴OC=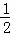 AB=OB,……………(2分)
AB=OB,……………(2分)
又∵CA=CB,∴∠CAB=∠B=45,∠1=∠2=45°,∠AOC=∠BOC=90°,
∴∠2=∠B,∵BN⊥DE,∴∠BND=90°,
又∵∠B=45°,∴∠3=45°,
∴∠3=∠B,∴DN=NB.……………(2分)
∵∠ACB=90°,∴∠NCM=90°.又∵BN⊥DE,∴∠DNC=90°
∴四边形DMCN是矩形,∴DN=MC,
∴MC=NB,……………(2分)
∴△MOC≌△NOB(SAS),……………(2分)
∴OM=ON,∠MOC=∠NOB,∴∠MOC﹣∠CON=∠NOB﹣∠CON,即∠MON=∠BOC=90°,
∴OM⊥ON.……………(2分)

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
 、
、 、
、 是一组距离不相等的平行线,作等边
是一组距离不相等的平行线,作等边 ,使
,使 、
、 在
在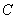 在
在 交
交 ,
, 的外接圆交
的外接圆交 ,试判断
,试判断 的形状并证明.
的形状并证明.
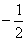
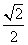 ①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在; ④使得M=1的x值是 或 .
①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在; ④使得M=1的x值是 或 .
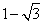 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P/(1,3)处.过点P/作x轴的平行线交抛物线于C、D两点,则翻折后的图案的高与宽的比为__________(结果可保留根号).
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P/(1,3)处.过点P/作x轴的平行线交抛物线于C、D两点,则翻折后的图案的高与宽的比为__________(结果可保留根号). ,
, ,a,b,其中a,b是方程
,a,b,其中a,b是方程 的两个根,则这4个数据的中位数是( )
的两个根,则这4个数据的中位数是( ) C.2 D.
C.2 D.
 p ,若存在请求出此时DM的长;不存在,请说明理由。
p ,若存在请求出此时DM的长;不存在,请说明理由。 