题目内容
【题目】如图,在直角坐标系中,三角形![]() 两顶点的坐标为
两顶点的坐标为![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上一动点(不与点
轴上一动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,
,![]() 分别平分
分别平分![]() .
.
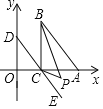
(1)当点![]() 在点
在点![]() 左边,三角形
左边,三角形![]() 的面积为6时,求点
的面积为6时,求点![]() 的坐标.
的坐标.
(2)当![]() 轴时,求
轴时,求![]() 的度数.
的度数.
(3)当点![]() 在点
在点![]() 右边时,写出
右边时,写出![]() 与
与![]() 的数量关系(不用说理).
的数量关系(不用说理).
【答案】(1)(2,0);(2)45°;(3)∠P=90°![]() ∠ACB,理由见详解.
∠ACB,理由见详解.
【解析】
(1)根据三角形面积公式求出AC,得到答案;
(2)根据角平分线的定义得到∠PBC=![]() ∠ABC,∠ACP=
∠ABC,∠ACP=![]() ∠ACE,根据三角形内角和定理计算即可;
∠ACE,根据三角形内角和定理计算即可;
(3)根据平行线的性质得到∠ACE=∠BAC,根据三角形内角和定理得到∠ABC-∠ACE=180°-∠ACB,根据角平分线的定义、三角形内角定理计算,得到答案.
解:(1)由题意得,![]() ×AC×4=6,
×AC×4=6,
解得,AC=3,
∴OC=OA-AC=2,
则点C的坐标为(2,0);
(2)∵BC⊥x轴,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
∵DE∥AB,
∴∠ACE=∠BAC,
∴∠ABC+∠ACE=90°,
∵PB,PC分别平分∠ABC,∠ACE,
∴∠PBC=![]() ∠ABC,∠ACP=
∠ABC,∠ACP=![]() ∠ACE,
∠ACE,
∴∠PBC+∠ACP=![]() (∠ABC+∠ACE)=45°,
(∠ABC+∠ACE)=45°,
∴∠P=180°-90°-45°=45°;
(3)∠P=90°![]() ∠ACB.
∠ACB.
如图:
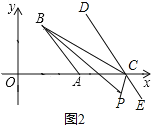
理由如下:∵DE∥AB,
∴∠ACE=∠BAC,
∴∠ABC-∠ACE=180°-∠ACB,
∵PB,PC分别平分∠ABC,∠ACE,
∴∠PBC=![]() ∠ABC,∠ACP=
∠ABC,∠ACP=![]() ∠ACE,
∠ACE,
∴∠PBC+∠ACP=![]() (∠ABC+∠ACE),
(∠ABC+∠ACE),
∴∠P=180°-∠PBC-∠ACP-∠ACB
=180°![]() (∠ABC+∠ACE)-∠ACB
(∠ABC+∠ACE)-∠ACB
=180°-90°+![]() ∠ACB-∠ACB
∠ACB-∠ACB
=90°![]() ∠ACB.
∠ACB.

【题目】某学校对学生暑假参加志愿服务的时间进行抽样调查,将收集的数据分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五组进行整理,并绘制成如下的统计图表(图中信息不完整).
五组进行整理,并绘制成如下的统计图表(图中信息不完整).

分组统计表
组别 | 志愿服务时间 | 人数 |
A |
|
|
B |
| 40 |
C |
|
|
D |
|
|
E |
| 16 |
请结合以上信息解答下列问题
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)补全“人数分组统计图①中![]() 组的人数和图②
组的人数和图②![]() 组和
组和![]() 组的比例值”;
组的比例值”;
(3)若全校学生人数为800人,请估计全校参加志愿服务时间在![]() 的范围的学生人数.
的范围的学生人数.


