Question

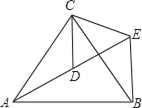
【题目】如图，在Rt△ABC中，AB＝3，BC＝4，动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q的运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止运动，连接PQ，设它们的运动时间为t（t＞0）秒．

（1）设△CBQ的面积为S，请用含有t的代数式来表示S；

（2）线段PQ的垂直平分线记为直线l，当直线l经过点C时，求AQ的长．

Answer 1

【答案】（1）S＝12﹣2t；（2）1.5

【解析】

（1）分0＜t≤3和3＜t≤5两种情况，表示出BQ的长度，根据三角形的面积公式可得；

（2）根据线段的垂直平分线的性质求出AP＝AQ，得出3﹣t＝t，求出即可.

解：（1）如图1，当0＜t≤3时，

BQ＝t，BC＝4，

∴S＝×4×t＝2t；

如图2，当3＜t≤5时，

，

AQ＝t﹣3，

则BQ＝3﹣（t﹣3）＝6﹣t，

∴S＝×4×（6﹣t）＝12﹣2t；

（2）如图3，

∵QP的垂直平分线过A，

∴AP＝AQ，

∴3﹣t＝t，解得t＝1.5；

或t﹣3＝t，显然不成立；

∴AP＝AQ＝1.5．