题目内容
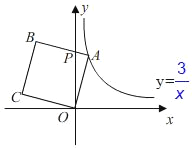
【题目】如图，点A在反比例函数y=
（x＞0）上，以OA为边作正方形OABC，边AB交y轴于点P，若PA：PB=1：2，则正方形OABC的面积=_____．
【答案】10.
【解析】
根据题意作出合适的辅助线，然后根据正方形的性质和反比例函数的性质，相似三角形的判定和性质、勾股定理可以求得AB的长．
由题意可得：OA=AB，设AP=a，则BP=2a，OA=3a，设点A的坐标为（m，
），作AE⊥x轴于点E．
∵∠PAO=∠OEA=90°，∠POA+∠AOE=90°，∠AOE+∠OAE=90°，∴∠POA=∠OAE，∴△POA∽△OAE，∴
=
，即
=
，解得：m=1或m=﹣1（舍去），∴点A的坐标为（1，3），∴OA=
，∴正方形OABC的面积=OA2=10．
故答案为：10．
练习册系列答案
相关题目
