题目内容
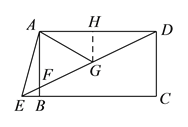
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 于点
于点![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(![]() )求证:
)求证:![]() .
.
(![]() )若
)若![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.

【答案】(![]() )见解析(
)见解析(![]() )
)![]()
【解析】试题分析:
(1)由已知条件易证∠GAD=∠ADE=∠CED,结合∠AGE=∠GAD+∠ADE,可得∠AGE=2∠CED,再结合∠AED=2∠CED即可得到∠AGE=∠AED,从而可得AE=AG;
(2)如下图,连接GH,由(1)中结论可知AE=AG=![]() ,结合BE=2,在Rt△ABE中可求得AB=11,结合BF=1可求得AF=10,再结合G是DF的中点,H是AD的中点由三角形中位线定理即可求得GH=5.
,结合BE=2,在Rt△ABE中可求得AB=11,结合BF=1可求得AF=10,再结合G是DF的中点,H是AD的中点由三角形中位线定理即可求得GH=5.
试题解析:
(![]() )∵ 四边形
)∵ 四边形![]() 是矩形,
是矩形,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,
又∵ ![]() 为
为![]() 中点,
中点,
∴ ![]() ,
,
∴ ![]() ,
,
∵∠AGE=∠GAD+∠ADE,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]() ,
,
![]() .
.
(![]() )连接
)连接![]() ,由(
,由(![]() )知:
)知:![]() =
=![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∵ ![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,
∴ ![]() .
.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目