题目内容
已知抛物线与x轴相交于两点A(1,0),B(-3,0),与y轴相交于点C(0,3).
(1)求此抛物线的函数表达式;
(2)如果点 是抛物线上的一点,求△ABD的面积.
是抛物线上的一点,求△ABD的面积.
【答案】
(1)抛物线的解析式为y=﹣(x﹣1)(x+3)(或y=﹣x2﹣2x+3);(2)△ABD的面积是 .
.
【解析】
试题分析:(1)根据题意可以设抛物线解析式为y=a(x﹣1)(x+3)(a≠0),然后把点C的坐标代入,即可求得a的值;
(2)根据三角形的面积公式进行求解.
试题解析:(1)∵抛物线与x轴相交于两点A(1,0),B(﹣3,0),
∴设抛物线解析式为y=a≠0).
∵抛物线与y轴相交于点C(0,3),
∴3=a(0﹣1)(0+3),
解得a=﹣1,
则抛物线的解析式为y=﹣(x﹣1)(x+3)(或y=﹣x2﹣2x+3);
(2)∵A(1,0),B(﹣3,0),
∴AB=4.
又∵ 是抛物线上的一点,
是抛物线上的一点,
∴m=﹣( ﹣1)(
﹣1)( +3)=﹣
+3)=﹣ ,
,
则△ABD的面积为: AB•|m|=
AB•|m|= ×4×
×4× =
= .
.
答:△ABD的面积是 .
.
考点:待定系数法求二次函数解析式.

练习册系列答案
相关题目
 如图,已知抛物线
如图,已知抛物线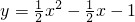 与x轴相交于点A、B,与y轴相交于C.
与x轴相交于点A、B,与y轴相交于C.
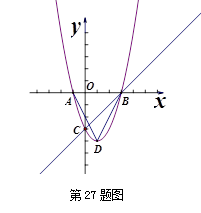
 (3) 探究:在抛物线的对称轴上是否存在点P,使⊙P与x轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
(3) 探究:在抛物线的对称轴上是否存在点P,使⊙P与x轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).