题目内容
如图, 已知抛物线 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).

(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为以AC为腰的等腰三角形,若存在,求点P的坐标,若不存在,说明理由.
(1) (2)(1,0)(3)P1(
(2)(1,0)(3)P1( ,-
,- )P2(-
)P2(- ,
, )P3(1, -2) P4(
)P3(1, -2) P4( ,-
,- ).
).
【解析】(1)∵二次函数 的图像经过点A(2,0)C(0,-1)
的图像经过点A(2,0)C(0,-1)
∴
 解得: b=-
解得: b=- c=-1 (2分)
c=-1 (2分)
∴二次函数的解析式为 (1分)
(1分)
(2)设点D的坐标为(m,0), (0<m<2)
∴ OD=m ∴AD=2-m
由△ADE∽△AOC得,
∴ ∴DE=
∴DE= (1分)
(1分)
∴△CDE的面积= ×
× ×m=
×m= =
= (2分)
(2分)
当m=1时,△CDE的面积最大,此时点D的坐标为(1,0) (1分)
(3)存在.
由(1)知:二次函数的解析式为
设y=0则 解得:x1=2 x2=-1
解得:x1=2 x2=-1 ,∴点B的坐标为(-1,0) C(0,-1)
,∴点B的坐标为(-1,0) C(0,-1)
设直线BC的解析式为:y=kx+b
∴  解得:k=-1 b=-1,∴直线BC的解析式为: y=-x-1
解得:k=-1 b=-1,∴直线BC的解析式为: y=-x-1
在Rt△AOC中,∠AOC=900
OA=2 OC=1,由勾股定理得:AC=
∵点B(-1,0) 点C(0,-1),∴OB=OC ∠BCO=450. (1分)
①当以点C为顶点且PC=AC= 时,
时,
设P(k, -k-1),过点P作PH⊥y轴于H,

∴∠HCP=∠BCO=450,CH=PH=∣k∣,在Rt△PCH中
k2+k2= 解得k1=
解得k1= ,
k2=-
,
k2=-
∴P1( ,-
,- ) P2(-
) P2(- ,
, )(3分)
)(3分)
②以A为顶点,即AC=AP=
设P(k, -k-1),过点P作PG⊥x轴于G,

AG=∣2-k∣ GP=∣-k-1∣
在Rt△APG中 AG2+PG2=AP2,(2-k)2+(-k-1)2=5 解得:k1=1,k2=0(舍) ∴P3(1, -2) (3分)
(3)AP=CP,此时AP²=CP²
2X²-2X+5=2X²
-2X=-5,X=2.5
代入BC方程,Y=-3.5
因此P4(2.5,-3.5)
综上所述,存在四点:P1( ,-
,- )P2(-
)P2(- ,
, )P3(1, -2) P4(
)P3(1, -2) P4( ,-
,- ).
).
(1)用待定系数法求得二次函数的解析式
(2)设点D的坐标为(m,0), (0<m<2),由△ADE∽△AOC得,
从而求得DE的长,通过△CDE的面积公式求得当m=1时,△CDE的面积最大,即可求出点D的坐标
(3)求出直线BC的解析式,若三角形为等腰三角形,则有三种可能,利用勾股定理从而求得P点的坐标
 |

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案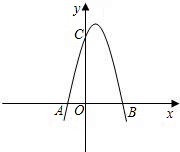 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).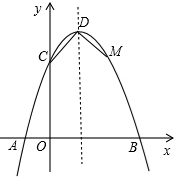 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1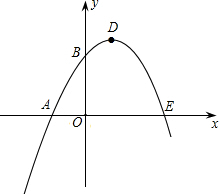 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )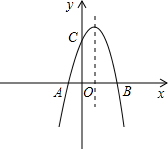 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).