题目内容
如图所示,AB是⊙○的一条弦,OD⊥AB,垂足为C,交⊙○于点D,点E在⊙○上,∠AOD=60°,OA=5.(1)求∠DEB的度数;(2)求弓形ADB的面积.

【答案】分析:(1)欲求∠DEB,又已知一圆心角,可利用圆周角与圆心角的关系求解.
(2)连接OB,根据Rt△AOC中∠AOC=60°,OA=5可求出AC及OC的长,再根据S弓形=S扇形AOB-S△AOB进行计算即可.
解答: 解:(1)∵OD⊥AB
解:(1)∵OD⊥AB
∴ =
= ,
,
∴∠DEB= ∠AOD=
∠AOD= ×60°=30°;
×60°=30°;
(2)连接OB,
∵Rt△AOC中∠AOC=60°,OA=5,
∴∠OAC=30°,OC= OA=
OA= ;AC=OA•cos∠OAC=5×
;AC=OA•cos∠OAC=5× =
= ,
,
∵OD⊥AB,AOD=60°,
∴∠AOB=2∠AOC=120°,
∴S弓形=S扇形AOB-S△AOB= -
- ×5
×5 ×
× =
= .
.
点评:本题考查了圆周角定理、垂径定理和扇形的面积的计算,要注意观察,从图中找到隐含条件解答.
(2)连接OB,根据Rt△AOC中∠AOC=60°,OA=5可求出AC及OC的长,再根据S弓形=S扇形AOB-S△AOB进行计算即可.
解答:
 解:(1)∵OD⊥AB
解:(1)∵OD⊥AB∴
 =
= ,
,∴∠DEB=
 ∠AOD=
∠AOD= ×60°=30°;
×60°=30°;(2)连接OB,
∵Rt△AOC中∠AOC=60°,OA=5,
∴∠OAC=30°,OC=
 OA=
OA= ;AC=OA•cos∠OAC=5×
;AC=OA•cos∠OAC=5× =
= ,
,∵OD⊥AB,AOD=60°,
∴∠AOB=2∠AOC=120°,
∴S弓形=S扇形AOB-S△AOB=
 -
- ×5
×5 ×
× =
= .
.点评:本题考查了圆周角定理、垂径定理和扇形的面积的计算,要注意观察,从图中找到隐含条件解答.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
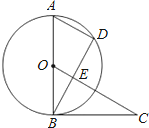 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.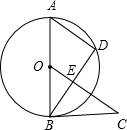 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.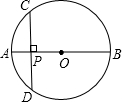 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为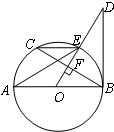 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )
如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )