题目内容
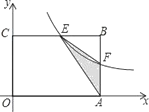
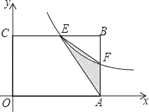
【题目】如图，在矩形OABC中，OA=6，OC=4，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数
的图象与BC边交于点E.
（1）当F为AB的中点时，求该函数的解析式；
（2）当k为何值时，△EFA的面积最大，最大面积是多少？
【答案】（1）该函数的解析式为y=
（x＞0）；（2）当k=12时，S有最大值，S最大=3.
【解析】如图，在矩形OABC中，OA=6，OC=4，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数
(k>0) 的图象与BC边交于点E.
（1）当F为AB的中点时，求该函数的解析式；
（2）当k为何值时，△EFA的面积最大，最大面积是多少？
试题分析：（1）当F为AB的中点时，点F的坐标为（3，1），由此代入求得函数解析式即可；
（2）根据图中的点的坐标表示出三角形的面积，得到关于k的二次函数，利用二次函数求出最值即可．
试题解析：（1）∵在矩形OABC中，OA=6，OC=4，∴B（6，4），
∵F为AB的中点，∴F（6，2），
又∵点F在反比例函数
（k＞0）的图象上，∴k=12，
∴该函数的解析式为y=
（x＞0）
（2）由题意知E，F两点坐标分别为E（
，4），F（6， 
），
∴
，
=
=
=
=
，
∴当k=12时，S有最大值．S最大=3．
【题目】某班一次数学测试成绩如下：
63, 84, 91, 53, 69, 81, 57, 69, 91, 78，
75, 81, 80, 67, 76, 81, 79, 94, 61, 69，
89, 70, 70, 87, 81, 86, 90, 88, 85, 67.
补充完整频数分布表：
成绩 |
|
|
|
|
|
频数 |
（2）补充完整图中的频数分布直方图：
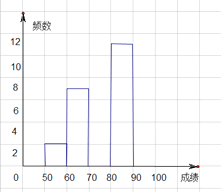
（3）若80分以上（含80分）的成绩为优秀，那么该班这次数学测验的优秀率是多少？
