题目内容
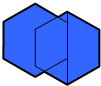如图，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形（阴影部分）外轮廓线的周长是________．
8
分析：根据图形特征分析出△ABD和△FGH为等边三角形，将图形（阴影部分）外轮廓线的周长转化为多边形周长问题解答．
解答：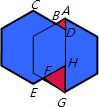
解：易得△ABD为等边三角形，
于是CB+BA=CB+BD=CD，
同理，EF+FG=EH，
所以阴影部分外轮廓线的周长共由八条长度等于边长线组成，则周长为8．
故答案为：8．
点评：此题考查了多边形的内角与外角和等边三角形的知识解答，体现了转化思想在解题中的作用．
分析：根据图形特征分析出△ABD和△FGH为等边三角形，将图形（阴影部分）外轮廓线的周长转化为多边形周长问题解答．
解答：
解：易得△ABD为等边三角形，于是CB+BA=CB+BD=CD，
同理，EF+FG=EH，
所以阴影部分外轮廓线的周长共由八条长度等于边长线组成，则周长为8．
故答案为：8．
点评：此题考查了多边形的内角与外角和等边三角形的知识解答，体现了转化思想在解题中的作用．
练习册系列答案
相关题目
10、如图，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形（阴影部分）外轮廓线的周长是（ ）
15、如图，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形（阴影部分）外轮廓线的周长是
