题目内容
(2012•海门市一模)关于x的方程kx2+(k-2)x+
=0有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程的两根分别为x1,x2,若|x1+x2|-1=x1x2,求k的值.
| k | 4 |
(1)求k的取值范围;
(2)设方程的两根分别为x1,x2,若|x1+x2|-1=x1x2,求k的值.
分析:(1)由关于x的方程有两个不相等的实数根,得到根的判别式大于0,且k不为0,列出关于k的不等式,求出不等式的解集即可得到k的范围;
(2)利用根与系数的关系表示出两根之和与两根之积,代入已知的等式中,得到关于k的方程,求出方程的解得到k的值,将求出的k值代入k的范围进行检验,即可得到满足题意的k的值.
(2)利用根与系数的关系表示出两根之和与两根之积,代入已知的等式中,得到关于k的方程,求出方程的解得到k的值,将求出的k值代入k的范围进行检验,即可得到满足题意的k的值.
解答:解:(1)由题意可得:
,
整理得:-4k+4>0,且k≠0,
解得:k<1,
则k的范围是k<1且k≠0;
(2)由题意可得:
,
∵|x1+x2|-1=x1x2,
∴|
|-1=
,即|
|=
,
∴
=
或
=-
,
解得:k=
或k=-8,
经检验k=
,k=-8满足题意,
则k的值是
或-8.
|
整理得:-4k+4>0,且k≠0,
解得:k<1,
则k的范围是k<1且k≠0;
(2)由题意可得:
|
∵|x1+x2|-1=x1x2,
∴|
| 2-k |
| k |
| 1 |
| 4 |
| 2-k |
| k |
| 5 |
| 4 |
∴
| 2-k |
| k |
| 5 |
| 4 |
| 2-k |
| k |
| 5 |
| 4 |
解得:k=
| 8 |
| 9 |
经检验k=
| 8 |
| 9 |
则k的值是
| 8 |
| 9 |
点评:此题考查了根与系数的关系,及根的判别式与方程解的情况,一元二次方程ax2+bx+c=0(a≠0),当b2-4ac>0时,方程有两个不相等的实数根;当b2-4ac<0时,方程无解;当b2-4ac=0时,方程有两个相等的实数根,且方程有解时,设方程的解分别为x1,x2,则有x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
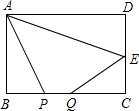 (2012•海门市一模)如图,矩形ABCD中,AB=4,BC=8,E为CD的中点,点P、Q为BC上两个动点,且PQ=3,当CQ=
(2012•海门市一模)如图,矩形ABCD中,AB=4,BC=8,E为CD的中点,点P、Q为BC上两个动点,且PQ=3,当CQ=