题目内容
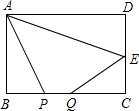（2012•海门市一模）如图，矩形ABCD中，AB=4，BC=8，E为CD的中点，点P、Q为BC上两个动点，且PQ=3，当CQ=| 5 |
| 3 |
| 5 |
| 3 |
分析：点A向右平移3个单位到M，点E关于BC的对称点F，连接MF，交BC于Q，要使四边形APQE的周长最小，只要AP+EQ最小就行，证△MNQ∽△FCQ即可．
解答：解：点A向右平移3个单位到M，点E关于BC的对称点F，连接MF，交BC于Q，
此时MQ+EQ最小，
∵PQ=3，DE=CE=2，AE=
=2
，
∴要使四边形APQE的周长最小，只要AP+EQ最小就行，
即AP+EQ=MQ+EQ过M作MN⊥BC于N，
设CQ=x，则NQ=8-3-x=5-x，
∵△MNQ∽△FCQ，
∴
=
∵MN=AB=4，CF=CE=2，CQ=x，QN=5-x，
解得：x=
，则CQ=
故答案为：
．
此时MQ+EQ最小，
∵PQ=3，DE=CE=2，AE=
| 82+22 |
| 17 |
∴要使四边形APQE的周长最小，只要AP+EQ最小就行，
即AP+EQ=MQ+EQ过M作MN⊥BC于N，
设CQ=x，则NQ=8-3-x=5-x，
∵△MNQ∽△FCQ，
∴
| MN |
| CF |
| NQ |
| CQ |
∵MN=AB=4，CF=CE=2，CQ=x，QN=5-x，
解得：x=
| 5 |
| 3 |
| 5 |
| 3 |
故答案为：
| 5 |
| 3 |
点评：本题考查了矩形的性质，勾股定理，轴对称-最短路线问题的应用，题目具有一定的代表性，但是一道难度偏大的题目，对学生提出较高的要求．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
