题目内容
 如图,CD∥AB,BF平分∠ABE,DE∥BF,若∠D=55°,则∠ABE=
如图,CD∥AB,BF平分∠ABE,DE∥BF,若∠D=55°,则∠ABE=
- A.110°
- B.115°
- C.125°
- D.135°
A
分析:过点E作直线EG∥CD,由CD∥AB可得AB∥CD∥EG,故可得出∠1=∠D=55°,所以∠3+∠2+∠FBE=180°,再由DE∥BF可知,∠1+∠2+∠FBE=180°,所以∠1=∠3=55°,再由BF平分∠ABE可知∠ABE=2∠3=110°.
解答: 解:过点E作直线EG∥CD,
解:过点E作直线EG∥CD,
∵CD∥AB,
∴AB∥CD∥EG,
∴∠1=∠D=55°,
∴∠3+∠2+∠FBE=180°,
∵DE∥BF,
∴∠1+∠2+∠FBE=180°,
∴∠1=∠3=55°,
∵BF平分∠ABE,
∴∠ABE=2∠3=110°.
故选A.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.
分析:过点E作直线EG∥CD,由CD∥AB可得AB∥CD∥EG,故可得出∠1=∠D=55°,所以∠3+∠2+∠FBE=180°,再由DE∥BF可知,∠1+∠2+∠FBE=180°,所以∠1=∠3=55°,再由BF平分∠ABE可知∠ABE=2∠3=110°.
解答:
 解:过点E作直线EG∥CD,
解:过点E作直线EG∥CD,∵CD∥AB,
∴AB∥CD∥EG,
∴∠1=∠D=55°,
∴∠3+∠2+∠FBE=180°,
∵DE∥BF,
∴∠1+∠2+∠FBE=180°,
∴∠1=∠3=55°,
∵BF平分∠ABE,
∴∠ABE=2∠3=110°.
故选A.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
相关题目
 18、如图,CD⊥AB于D,DE∥BC,∠1=∠2,则FG与AB的位置关系是
18、如图,CD⊥AB于D,DE∥BC,∠1=∠2,则FG与AB的位置关系是 26、如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
26、如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,试判断DG与BC的位置关系,并说明理由. 12、如图,CD⊥AB,D为垂足,∠CDE=30°,则∠BDE=
12、如图,CD⊥AB,D为垂足,∠CDE=30°,则∠BDE=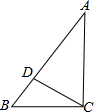 如图,CD⊥AB于D,AC=20,BC=15,DB=9.
如图,CD⊥AB于D,AC=20,BC=15,DB=9. 已知:如图,CD⊥AB,交点为点D,BE⊥AC,交点为点E,BE、CD交于点O,且AO平分∠BAC.试问:OB与OC有何大小关系,并说明理由.
已知:如图,CD⊥AB,交点为点D,BE⊥AC,交点为点E,BE、CD交于点O,且AO平分∠BAC.试问:OB与OC有何大小关系,并说明理由.