题目内容
甲商场销售世博吉祥物海宝,每个成本价为8元.市场调查发现,在一段时间内,销售量y(个)随销售单价x(元/个)的变化而变化,y和x是一次函数的关系,设海宝在这段时间内平均每天的销售利润为w(元),解答下列问题:
(1)求y与x的关系式和w与x的关系式;
(2)当销售单价为何值时,每天的销售利润最大?最大有多大?
(3)如果物价部门规定海宝的销售单价不得高于15元/个,商场想要在这段时间内每天平均获得320元的销售利润,销售单价应定为多少元?
| x(元) | … | 10 | 12 | 14 | … |
| y (个) | … | 100 | 80 | 60 | … |
(2)当销售单价为何值时,每天的销售利润最大?最大有多大?
(3)如果物价部门规定海宝的销售单价不得高于15元/个,商场想要在这段时间内每天平均获得320元的销售利润,销售单价应定为多少元?
考点:二次函数的应用
专题:
分析:(1)根据表格里有待定系数法能够确定一次函数的解析式;根据总利润=单件销售利润×销量即可得到w与x之间的函数关系;
(2)将二次函数配方后即可确定最值;
(3)代入w=320得到有关x方程即可求得x的值.
(2)将二次函数配方后即可确定最值;
(3)代入w=320得到有关x方程即可求得x的值.
解答:解:(1)∵销售量y(个)随销售单价x(元/个)的变化而变化,y和x是一次函数的关系,
∴设一次函数的关系式为y=kx+b,
由表格知:
,
解得:
,
∴一次函数的解析式为y=-10x+200;
w=(x-8)y=(x-8)(-10x+200)=-10x2+280x-1600;
(2)∵w=-10x2+280x-1600=-10(x-14)2+360,
∴销售单价为14元时,每天的销售利润最大,最大有360元;
(3)由题意得:-10(x-14)2+360=320,
解得:x=12或x=16,
∵销售单价不能高于15元,
∴x=12,
∴销售单件为12元,利润能达到320元.
∴设一次函数的关系式为y=kx+b,
由表格知:
|
解得:
|
∴一次函数的解析式为y=-10x+200;
w=(x-8)y=(x-8)(-10x+200)=-10x2+280x-1600;
(2)∵w=-10x2+280x-1600=-10(x-14)2+360,
∴销售单价为14元时,每天的销售利润最大,最大有360元;
(3)由题意得:-10(x-14)2+360=320,
解得:x=12或x=16,
∵销售单价不能高于15元,
∴x=12,
∴销售单件为12元,利润能达到320元.
点评:本题考查了二次函数的应用,解题的关键是能够从实际问题中抽象出二次函数模型,难度不大.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
下列说法,正确的是( )
| A、经过一点有且只有一条直线 |
| B、两点确定一条直线 |
| C、两条直线相交至少有两个交点 |
| D、线段AB就是表示点A到点B的距离 |
 如图,BD=DC,AB=AC,∠BAC=70°,则∠BAD=( )
如图,BD=DC,AB=AC,∠BAC=70°,则∠BAD=( )| A、40° | B、70° |
| C、30° | D、35° |
 已知二次函数y=x2+bx-1的图象经过点(3,2).
已知二次函数y=x2+bx-1的图象经过点(3,2). 如图,该图中不同的线段数共有
如图,该图中不同的线段数共有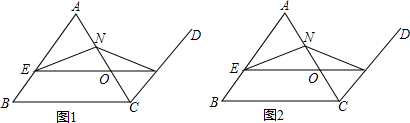
 如图,是由几个大小相同的小正方体所搭成的几何体从上面看到的形状图,小正方形中的数字表示在这个位置小正方体的个数,则从正面看到的这个几何体的形状图是( )
如图,是由几个大小相同的小正方体所搭成的几何体从上面看到的形状图,小正方形中的数字表示在这个位置小正方体的个数,则从正面看到的这个几何体的形状图是( )


